Đáp án: A

- Miêu tả sẽ khiến cho văn bản thêm sinh động, dễ hình dung và giàu sức sống.

- Còn thuyết mình giúp cho văn bản cụ thể, rõ ràng và rành mạch.

Cách đơn giản để xác định được bộ phận nào có trong loa có từ tính là đưa một miếng sắt hoặc thép vào các bộ phận có trong loa, bộ phận nào hút thanh sắt hoặc thanh thép thì bộ phận đó có từ tính.

sờ tay vào loa r bật âm thanh  lên phàn nào rung thì phần đó phát ra âm thanh

Tham khảo:

Theo định lí cosin ta có:

\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\end{array}\)

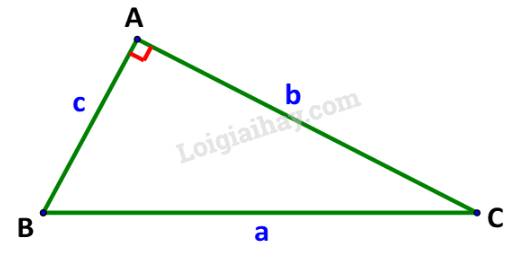
Mà \(\cos A = \cos {90^o} = 0;\cos B = \frac{c}{a};\;\cos C = \frac{b}{a}\)

 \( \Rightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.0\\{b^2} = {a^2} + {c^2} - \,2a\,c.\frac{c}{a}\\{c^2} = {b^2} + {a^2} - \,2ab.\frac{b}{a}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2}\\{b^2} = {a^2} + {c^2} - \,2{a^2}\\{c^2} = {b^2} + {a^2} - \,2{b^2}\end{array} \right. \Leftrightarrow {a^2} = {b^2} + {c^2}\)

Vậy định lí Pythagore là một trường hợp đặc biệt của định lí cosin.

Đoạn văn tham khảo:

      Đoạn trích Vĩnh biệt Cửu Trùng Đài cùng với bi kịch của Vũ Như Tô đã nhắc nhở mỗi chúng ta về ước mơ chân chính trong cuộc sống. Con người chúng ta từ khi sinh ra cho tới lúc trưởng thành, ai cũng có một ước mơ, hoài bão của riêng mình. Ước mơ giúp chúng ta có thể sống vui vẻ, có ý nghĩa và mục đích, khi thực hiện được ước mơ của mình con người cảm thấy được thành quả của quá trình nỗ lực cố gắng đúng như dân gian ta thường nói “Sống là phải có ước mơ”. Ước mơ là gì? Nó chính là những dự định, khát khao mà mỗi chúng ta mong muốn đạt được trong thời gian ngắn hoặc dài. Là mong muốn được cống hiến sức lực của mình cho xã hội và khi chúng ta đạt được ước mơ cũng là lúc chúng ta được thừa nhận năng lực của mình. Nếu không có ước mơ bạn sẽ không xác định được mục tiêu sống của mình là gì. Chính vì không xác định được phương hướng sẽ dẫn tới bạn sẽ sống hoài sống phí, và trở thành người tụt hậu bị bạn bè, xã hội bỏ lại phía sau. Con đường dẫn tới ước mơ cũng vô cùng khó khăn, không phải lúc nào cũng dễ dàng đạt được, nhưng với những người kiên trì, bền chí, thì ước mơ sẽ giúp cho bạn định hướng cho tương lai của mình một cách tốt đẹp nhất. Là một học sinh ngồi trên ghế nhà trường chúng ta cần phải có ước mơ mục đích sống cho riêng mình. Để đạt được ước mơ chúng ta cần ra sức rèn luyện học tập, tu dưỡng đạo đức để chuẩn bị những tư trang cần thiết cho con đường đi tới ước mơ của mình.

??????????????????

Trong một tam giác, bình phương một cạnh bằng tổng bình phương của hai cạnh kia, trừ hai lần tích của chúng và côsin của góc xen giữa hai cạnh đó.

Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)

Và nửa chu vi là: \(\frac{{441 + 575 + 538}}{2} = 777(m)\)

Do đó: \({S_{CDB}} = \sqrt {777.\left( {777 - 441} \right).\left( {777 - 575} \right).\left( {777 - 538} \right)}  \approx 112267,7\left( {{m^2}} \right)\)

Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)

Và nửa chu vi là: \(\frac{{217 + 476 + 538}}{2} = 615,5(m)\)

Do đó: \({S_{DBE}} = \sqrt {615,5.\left( {615,5 - 217} \right).\left( {615,5 - 476} \right).\left( {615,5 - 538} \right)}  \approx 51495,13\left( {{m^2}} \right)\)

Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)

Và nửa chu vi là: \(\frac{{401 + 476 + 256}}{2} = 566,5(m)\)

Do đó: \({S_{ABE}} = \sqrt {566,5.\left( {566,5 - 401} \right).\left( {566,5 - 476} \right).\left( {566,5 - 256} \right)}  \approx 51327,97\left( {{m^2}} \right)\)

Vậy diện tích S của ngũ giác ABCDE là: \(S = {S_{CDB}} + {S_{DBE}} + {S_{ABE}} \approx 112267,7 + 51495,13 + 51327,97 = 215090,8\left( {{m^2}} \right)\)

Chú ý

+) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”

+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.

1. Hoàn thành
2. Chưa hoàn thành
3. Hoàn thành
4. Hoàn thành

Định lí cosin: Trong tam giác ABC

\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\quad (3)\end{array}\)

Ta có \((1) \Leftrightarrow 2bc\cos A = {b^2} + {c^2} - {a^2}\, \Leftrightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}\,}}{{2b\,c}}.\)

Tương tự từ (2) và (3) ta suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\); \(\cos C = \frac{{{b^2} + {a^2} - {c^2}\,}}{{2b\,a}}\)