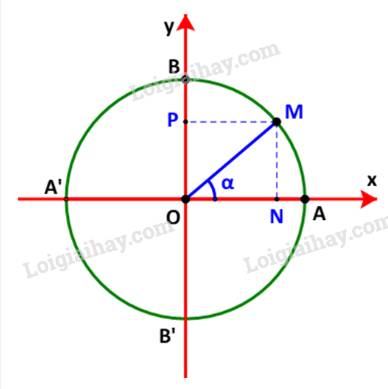
Đơn giản các biểu thức sau:
a) \(\sin {100^o} + \sin {80^o} + \cos {16^o} + \cos {164^o};\)
b) \(2\sin \left( {{{180}^o} - \alpha } \right).\cot \alpha - \cos \left( {{{180}^o} - \alpha } \right).\tan \alpha .\cot \left( {{{180}^o} - \alpha } \right)\) với \({0^o} < \alpha < {90^o}\).