Vẽ đồ thị mỗi hàm số bậc hai sau:
a) \(y = {x^2} - 4x - 3\)
b) \(y = {x^2} + 2x + 1\)
c) \(y = - {x^2} - 2\)
Vẽ đồ thị các hàm số bậc hai sau:
a) \(y = - {x^2} + 4x - 3\)
b) \(y = {x^2} + 2\)
c) \(y = \frac{1}{2}{x^2} + x + 1\)
d) \(y = {x^2} - 4x + 4\)
a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
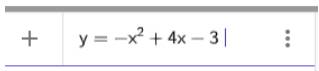
Ta có ngay parabol trên vùng làm việc như hình dưới:
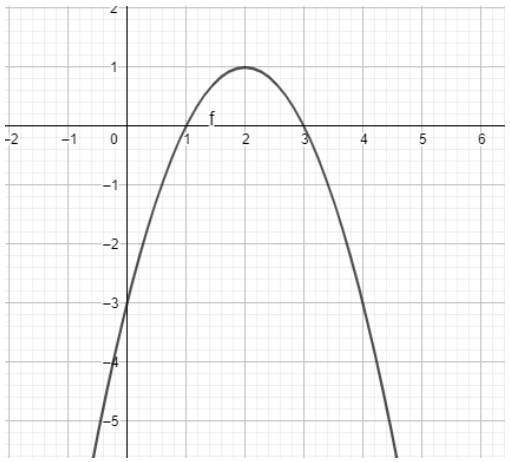
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
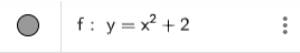
Ta có ngay parabol trên vùng làm việc như hình dưới:
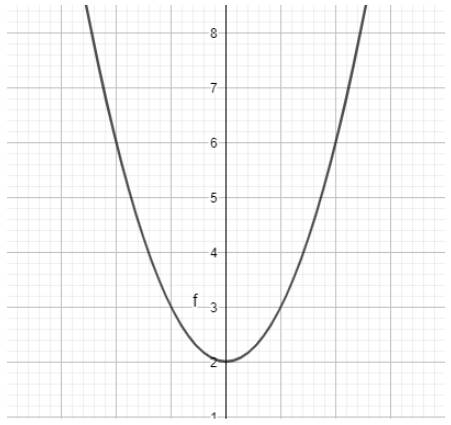
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
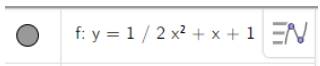
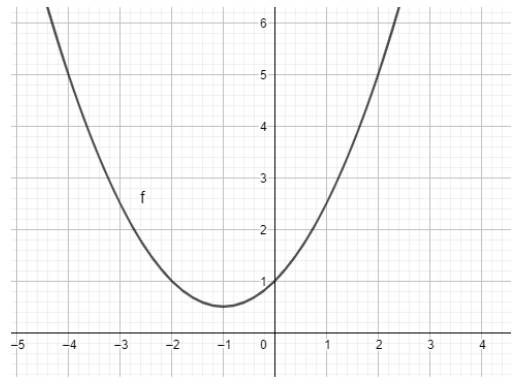
Ta có ngay parabol trên vùng làm việc như hình dưới:
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
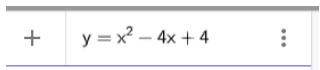
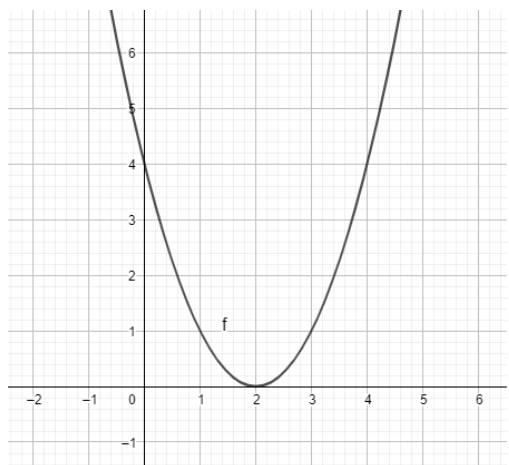
Ta có ngay parabol trên vùng làm việc như hình dưới:
Vẽ đồ thị các hàm số sau:
a) \(y = {x^2} - 4x + 3\)
b) \(y = - {x^2} - 4x + 5\)
c) \(y = {x^2} - 4x + 5\)
d) \(y = - {x^2} - 2x - 1\)
Tham khảo:
a)
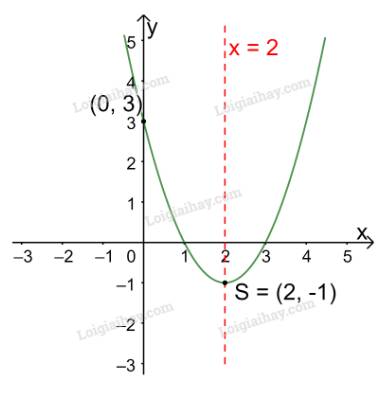
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
b)
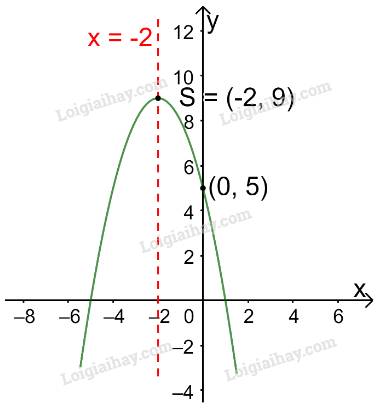
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.( - 1)}} = - 2;{y_S} = - {( - 2)^2} - 4.( - 2) + 5 = 9.\)
+ Có trục đối xứng là đường thẳng \(x = - 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
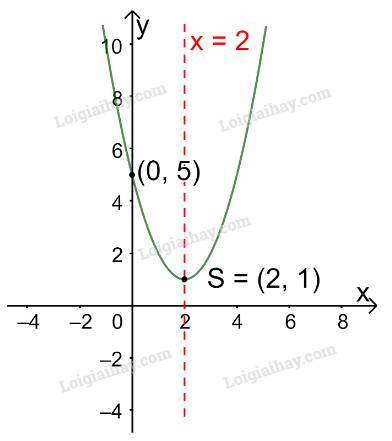
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 5 = 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
d)
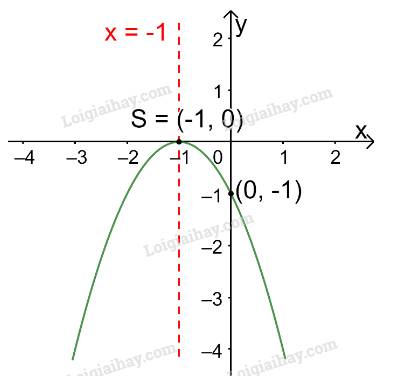
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 2x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 2)}}{{2.( - 1)}} = - 1;{y_S} = - {( - 1)^2} - 2.( - 1) - 1 = 0\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua gốc tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
Vẽ đồ thị của mỗi hàm số sau:
a) \(y = {x^2} - 3x - 4\)
b) \(y = {x^2} + 4x + 4\)
c) \(y = - {x^2} + 2x - 2\)
Tham khảo:
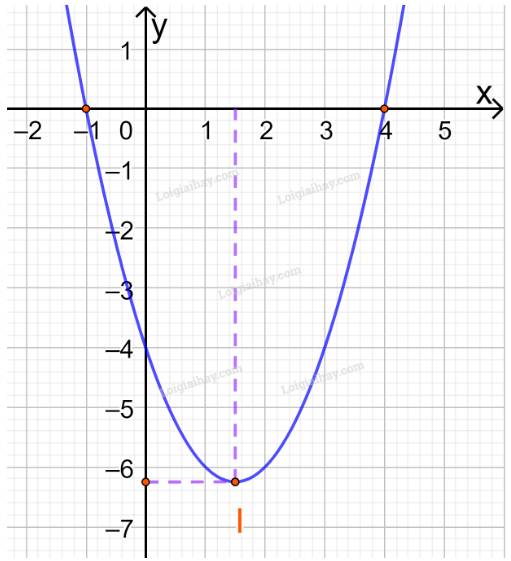
a) \(y = {x^2} - 3x - 4\)
Đồ thị hàm số có đỉnh \(I\left( {\dfrac{3}{2}; - \dfrac{{25}}{4}} \right)\)
Trục đối xứng là \(x = \dfrac{3}{2}\)
Giao điểm của parabol với trục tung là (0;-4)
Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
Điểm đối xứng với điểm (0;-4) qua trục đối xứng \(x = \frac{3}{2}\) là (3;-4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
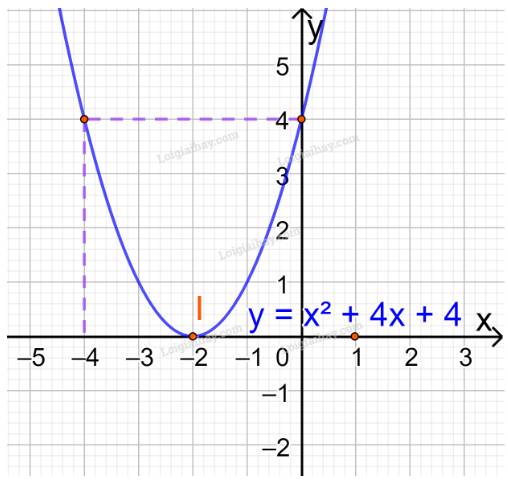
b) \(y = {x^2} + 4x + 4\)
Đồ thị hàm số có đỉnh \(I\left( { - 2;0} \right)\)
Trục đối xứng là \(x = - 2\)
Giao điểm của parabol với trục tung là (0;4)
Giao điểm của parabol với trục hoành là I(-2;0)
Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = - 2\) là (-4;4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
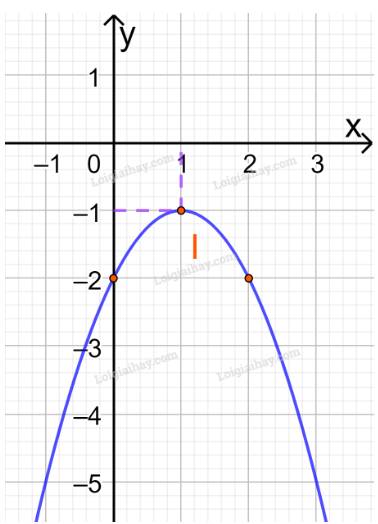
c) \(y = - {x^2} + 2x - 2\)
Đồ thị hàm số có đỉnh \(I\left( {1; - 1} \right)\)
Trục đối xứng là \(x = 1\)
Giao điểm của parabol với trục tung là (0;-2)
Điểm đối xứng với điểm (0;-2) qua trục đối xứng \(x = 1\) là (2;-2)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
Vẽ đồ thị các hàm số sau:
a) \(y = 2{x^2} + 4x - 1\)
b) \(y = - {x^2} + 2x + 3\)
c) \(y = - 3{x^2} + 6x\)
d) \(y = 2{x^2} - 5\)
Tham khảo:
a)
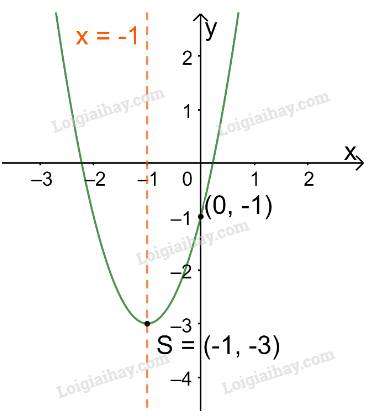
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
b)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.

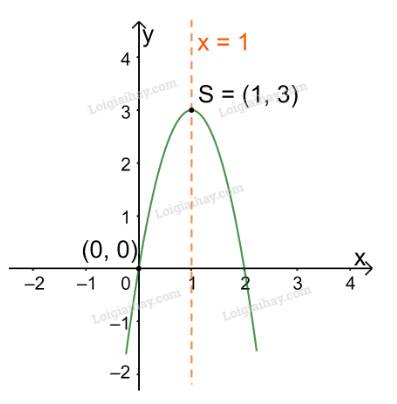
c)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
d)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.

Viết mỗi hàm số sau đây dưới dạng hàm số bậc nhất trên từng khoảng sau đó vẽ đồ thị và lập bảng biến thiên:
a) y = |x - 2| - 2x
b) y = -2|x - 1|
c) y = |x - 1| - |2x - 4|
d) y = 2|x + 2| - |x| + 1
Câu 12. Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
A. y = x 2 − 3x + 2. B. y = 2x 2 − 4x + 3. C. y = x 2 − 2x. D. y = x 2 + 2x
Cho các hàm số bậc nhất hãy xác định hệ số a,b của chúng:
y = -3x + 2 (a = ... ; b = ...)
y = 5x (a = ... ; b = ...)
y = 1 + 4 (a = ... ; b = ...)
C2:
vẽ đồ thị các hàm số sau:
a. y= 2x + 1
b. y = -x + 2
Câu 1:
y=-3x+2
a=-3; b=2
y=5x
a=5; b=0
Vẽ đồ thị của mỗi hàm số sau:
a) \(y = 2{x^2} - 6x + 4\)
b) \(y = - 3{x^2} - 6x - 3\)
Tham khảo:
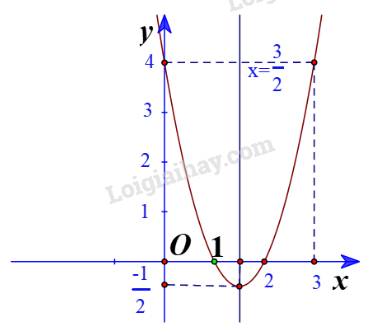
a) Hàm số có \(a = 2,b = - 6;c=4 \) \(\Rightarrow - \frac{b}{{2a}} = - \frac{{ - 6}}{{2.2}} = \frac{3}{2}; y\left( {\frac{3}{2}} \right) = 2{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 4 = - \frac{1}{2} \)
+ Đồ thị hàm số có đỉnh \(I\left( {\frac{3}{2}; - \frac{1}{2}} \right)\)
+ Trục đối xứng là \(x = \frac{3}{2}\)
+ Giao điểm của parabol với trục tung là (0;4)
+ Giao điểm của parabol với trục hoành là (2;0) và (1;0)
+ Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = \frac{3}{2}\) là \(\left( {3;4} \right)\)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
b) Hàm số có \(a = -3,b = - 6;c=-3 \) \(\Rightarrow - \frac{b}{{2a}} = - \frac{{ - 6}}{{2.(-3)}} =-1 ; y(-1) = - 3{(-1)^2} - 6.(-1) - 3 = 0 \)
+ Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\)
+ Trục đối xứng là \(x = - 1\)
+ Giao điểm của parabol với trục tung là (0;-3)
+ Giao điểm của parabol với trục hoành là \(I\left( { - 1;0} \right)\)
+ Điểm đối xứng với điểm (0;-3) qua trục đối xứng \(x = - 1\) là (-2;-3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|