Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình bình hành.

Những câu hỏi liên quan
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhấtA. ba điểm phân biệtB. 1 điểm và 1 đường thẳngC. 2 đường thẳng cắt nhauD. 4 đ...
Đọc tiếp
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên
2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên
3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là
4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên
5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên
6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhất
A. ba điểm phân biệt
B. 1 điểm và 1 đường thẳng
C. 2 đường thẳng cắt nhau
D. 4 điểm phân biệt
1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C
Đúng 0
Bình luận (0)
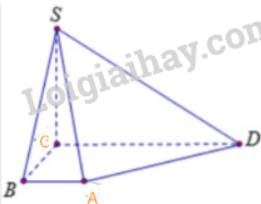
Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình thang, AB song song với CD và AB = 2cm, CD = 6cm.
Tham khảo:
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng các mặt bên là hình tam giác
Hình thang ABCD có AB//CD và AB=2cm, CD=6cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba đáy BC
Từ đó, ta vẽ được hình biểu diễn của S.ABCD.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I là trung điểm của SA, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là A. Tam giác IBC. B. Hình thang IJCB (J là trung điểm SD ). C. Hình thang IGBC (G là trung điểm SB ). D. Tứ giác IBCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I là trung điểm của SA, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là
A. Tam giác IBC.
B. Hình thang IJCB (J là trung điểm SD ).
C. Hình thang IGBC (G là trung điểm SB ).
D. Tứ giác IBCD
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
Trong các phát biểu sau, phát biểu nào đúng?a) Hình chóp đều S.ABCD có đáy là hình bình hành.b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Đọc tiếp
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, N lần lượt là trung điểm của SA, SC (tham khảo hình vẽ). Tìm giao tuyến d của hai mặt phẳng (BIN) và (ABCD) A. d là đường thẳng đi qua B và song song với AC B. d là đường thẳng đi qua S và song song với AD C. d là đường thẳng đi qua B và song song với CD D. d là đường thẳng đi qua hai điểm I, N
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, N lần lượt là trung điểm của SA, SC (tham khảo hình vẽ). Tìm giao tuyến d của hai mặt phẳng (BIN) và (ABCD)
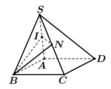
A. d là đường thẳng đi qua B và song song với AC
B. d là đường thẳng đi qua S và song song với AD
C. d là đường thẳng đi qua B và song song với CD
D. d là đường thẳng đi qua hai điểm I, N
![]()
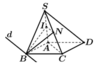
Ta có IN là đường trung bình của ∆ S A C nên IN//AC
Lại có ![]()
Do đó: IN//AC//d
Vậy giao tuyến của hai mặt phẳng (BIN) và (ABCD) là đường thẳng d đi qua B và song song với AC
Chọn A.
Đúng 0
Bình luận (0)
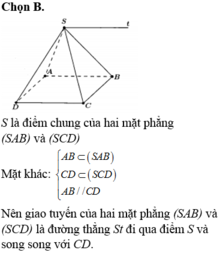
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của (SBA) và (SCD) là A. Đường thẳng qua S và song song với AD B. Đường thẳng qua S và song song với CD C. Đường SO với O là tâm hình bình hành D. Đường thẳng qua S và cắt AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của (SBA) và (SCD) là
A. Đường thẳng qua S và song song với AD
B. Đường thẳng qua S và song song với CD
C. Đường SO với O là tâm hình bình hành
D. Đường thẳng qua S và cắt AB
Hình chóp S.ABCD có đáy là hình bình hành ABCD. Giả sử M thuộc đoạn thẳng SB. Mặt phẳng (ADM) cắt hình chóp S.ABCD theo thiết diện là hình:
A.tam giác
B. hình thang
C. hình bình hành
D.hình thoi
Do AD//BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC, đường thẳng này cắt SC tại N.
Ta có MN//AD. Vậy thiết diện là hình thang AMND.
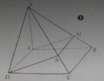
Đáp án B
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì?
A. tam giác
B. hình bình hành
C. hình thang
D. hình thoi
Vì CD ⊂ (MCD), CD // AB, AB ⊂ (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.
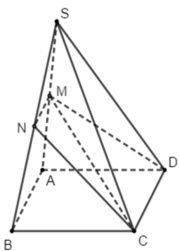
Đáp án C
Đúng 0
Bình luận (0)