Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết \(\widehat A\)= \({110^o}\).

Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
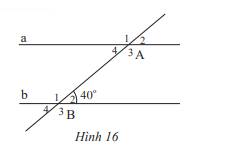
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Cho tứ giác ABCD có \(\widehat{B}=110^o;\widehat{C}=120^o;\widehat{D}=60^o\)
a) Tính góc A
b) Chứng minh tứ giác ABCD là hình thang
c) Gọi M,N lần lượt là trung điểm của AB và CD. Biết BC=8cm,AD=12cm. Tính độ dài đoạn thẳng MN
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác \(OMN\) vuông cân tại \(O\). Tính góc giữa hai thanh gỗ \(a\) và \(b\).

Ta có:\(a||OM\Rightarrow\left(a,b\right)=\left(OM,b\right)=\widehat{MON}=90^o\).
Cho hình thang vuông ABCD, có \(\widehat{A}\), \(\widehat{D}\) vuông và AB = 15cm; AD = 20cm, biết AC và BD vuông góc với nhau ở O. Tính diện tích hình thang ABCD
Tính các góc của hình thang ABCD , có đáy là AB , CD . Biết rằng
a) \(\widehat{A}-\widehat{D}=20^o;\widehat{B}=2\widehat{C}\)
b) \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}=20^o\)
a: góc A-góc D=20 độ
góc A+góc D=180 độ
=>góc A=(20+180)/2=100 độ và góc D=180-100=80 độ
góc B=2*góc C
góc B+góc C=180 độ
=>góc B=2/3*180=120 độ; góc C=180-120=60 độ
b: góc B-góc C=20 độ
góc B+góc C=180 độ
=>góc B=(180+20)/2=100 độ và góc C=80 độ
=>góc A=100+20=120 độ
=>góc D=60 độ
Tính các góc của hình thang cân, biết một góc bằng 40o và \(\widehat{A}\) = \(\widehat{B}\) = 180o - \(\widehat{C}\) = 140o.
\(\widehat{A}=\widehat{B}=180^0-\widehat{C}=140^0\)
=>\(\widehat{C}=180^0-140^0=40^0\) và \(\widehat{A}=\widehat{B}=140^0\)
\(\widehat{C}=\widehat{D}=40^0\)
Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.
a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)
b) \(\widehat P = \widehat Q = 110^\circ \)
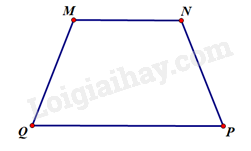
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)
Tính các góc của hình bình hành ABCD, biết :
a) \(\widehat{A}=110^0\)
b) \(\widehat{A}-\widehat{B}=20^0\)
a) \(\widehat{A}=\widehat{C}=110^0;\widehat{B}=\widehat{D}=70^0\)
b) \(\widehat{A}=\widehat{C}=100^0;\widehat{B}=\widehat{D}=80^0\)
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là 30 0 , chiều dài mỗi bên dốc mái là 3,5m. Tính gần đúng bề rộng của mái nhà.
A. 6,52m
B. 6,06m
C. 5,86m
D. 5,38m
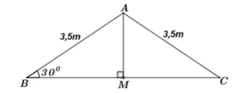
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: ∆ ABC cân tại A
![]()
Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC.
Gọi M là trung điểm của BC.
=> AM là đường trung tuyến đồng thời là đường cao của ABC (tính chất).
Xét ∆ ABM vuông tại M ta có:
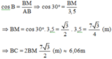
Vậy bề rộng mái nhà là 6,06m
Đáp án cần chọn là: B