Cho Hình 3.44. Giải thích tại sao:
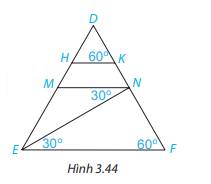
a) MN//EF
b) HK//EF
c) HK//MN
Cho Hình 3.43. Giải thích tại sao:

a) Ax’ // By b) By \( \bot \) HK
a) Vì \(\widehat {xAB} = \widehat {ABy}( = 45^\circ )\)
Mà hai góc này ở vị trí so le trong
Do đó, xx’ // By ( Dấu hiệu nhận biết 2 đường thẳng song song) hay Ax’ // By
b)
Cách 1:
Vì Ax’ // By nên \(\widehat{x'HK}=\widehat{HKB}\) (2 góc so le trong)
Mà \(\widehat{x'HK}=90^0\) nên \(\widehat{HKB}=90^0\)
Do đó, Ax’ \( \bot \) HK
Cách 2:
Vì Ax’ // By, mà By \( \bot \) HK nên Ax’ \( \bot \) HK (đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia)
Cho tam giác ABC nhọn, có 3 đường cao AD, BE, CF cắt nhau tại H. Gọi M, N là
trung điểm của BC và AH. Gọi I là giao điểm của MN và EF,đường phân giác góc A cắt MN tại K.
a)CMR: MN vuông góc với EF
b)CMR: NHI = HMI
c) CMR: HK là phân giác góc EHC.
cho tam giác abc có 2 đường trung tuyến BM,CN cắt nhau tại G gọi E,F lần lượt là các trung diểm của các đoạn BG,CG cmr:
a)MN=EF
b)MN//EF
c)NE=MF
d)NE//Mf
\(a,b,\) Ta có \(\left\{{}\begin{matrix}AN=BN\\AM=CM\end{matrix}\right.\Rightarrow MN\) là đtb \(\Delta ABC\Rightarrow MN//BC;MN=\dfrac{1}{2}BC\left(1\right)\)
Ta có \(\left\{{}\begin{matrix}BE=EG\\CG=GF\end{matrix}\right.\Rightarrow EF\) là đtb \(\Delta BGC\Rightarrow EF//BC;EF=\dfrac{1}{2}BC\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow EF=MN;EF//MN\)
\(c,d,\) Cmtt câu a,b, ta được \(NE,MF\) lần lượt là đtb \(\Delta AGB;\Delta AGC\)
\(\Rightarrow\left\{{}\begin{matrix}NE=\dfrac{1}{2}AG;NE//AG\\MF=\dfrac{1}{2}AG;MF//AG\end{matrix}\right.\Rightarrow NE=MF;NE//MF\)
cho tam giác MNP cân tại P. Gọi H là trung điểm của MN. K là hình chiếu của H trên PM. Đường thẳng qua P và vuông góc với NK cắt HK tại I. Chứng minh rằng I là trung điểm của HK.
Mk dang can gap mn giup mk voi
A)cho biết MN/HK=9/4,MN=18cm. Hãy tính HK
Ta có: \(\dfrac{MN}{HK}=\dfrac{9}{4}\)
\(\Rightarrow\dfrac{18}{HK}=\dfrac{9}{4}\)
\(\Rightarrow9.HK=18.4\)
\(\Rightarrow9HK=72\)
\(\Rightarrow HK=8cm\)
Cho tam giác ABC có BC = 12 cm, Trung tuyến BM và CN cắt nhau tại G.
Gọi H, K theo thứu tự là trung điểm của BG và CG.
a) Tính MN
b) Chứng minh MN // HK và MN = HK
a, vì BM,CN là các trung tuyến=>AN=NB
và AM=MC=>MN là đường trung bình tam giác ABC
=>MN//BC(1)
\(=>MN=\dfrac{1}{2}BC=6cm\)
b, có H,K theo theo thứ tự là trung điểm của BG và CG.
=>GH=HB và GK=KC
=>HK là đường trung bình tam giác GBC=>HK//BC(2)
(1)(2)=>HK//MN
=>\(HK=\dfrac{1}{2}BC=>HK=MN\left(=\dfrac{1}{2}BC\right)\)
Cho tam giác ABC vuông tại A có 2 đường trung tuyến BM và CN cắt nhau tại G. Gọi H,K lần lượt là trung điểm của GB và GC.
a) Chứng minh: MN//HK, MN=HK.
b) Tính HK biết AB=9cm; AC=12cm.
a) Xét ΔABC có
N là trung điểm của AB(CN là đường trung tuyến ứng với cạnh AB của ΔABC)
M là trung điểm của AC(BN là đường trung tuyến ứng với cạnh AC của ΔABC)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒MN//BC và \(MN=\frac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
H là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: HK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
⇒HK//BC và \(HK=\frac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra MN//HK và MN=HK(đpcm)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
\(\Leftrightarrow BC=\sqrt{225}=15cm\)
\(\Leftrightarrow2\cdot HK=15cm\)
hay \(HK=\frac{15cm}{2}=7.5cm\)
Vậy: HK=7,5cm
Mn ơi.Mk ms tạo hk liệu.Mong mn đăng ký ủng hộ nha: Lớp hk giải trí
Cho hình thang cân MNHK(NM//HK,MN<HK),kéo dài MK cắt MH tại i.
a)Chướng minh INM là tam giác cân
b)Gọi NH cắt MK tại O.Chứng minh IO vuông góc với HKgiup to nha !! to dang can gap lam
Sửa đề: NK cắt MH tại I.
a) Ta có:
góc INM + góc KNM = 180 độ ( 2 góc kề bù)
góc IMN + góc HMN = 180 độ ( 2 góc kề bù)
góc KNM = góc HMN ( định nghĩa hình thang cân NMHK)
=> góc INM = góc IMN
=> tam giác INM cân tại I.
b) Gọi F là trung điểm của NM.
Xét tam giác INM cân tại I có IF là đường trung tuyến cũng là đường cao và là đường phân giác
=> IF vuông góc với NM tại F (1)
Xét tam giác NMK và tam giác MNH ta có:
NM là cạnh chung
góc MNK = góc NMH ( định nghĩa hình thang cân NMHK)
NK = MH ( tính chất hình thang cân NMHK)
=> tam giác NMK = tam giác MNH ( c - g - c)
=> góc NMK = góc MNH ( 2 góc tương ứng)
=> tam giác ONM cân tại O
Mà Ò là đường trung tuyến nên cũng là đường cao
=> OF vuông góc với NM tại F (2)
Từ (1) và (2) suy ra IF trùng với OF ( Tiên đề Ơ - clit)
=> I, F, O thẳng hàng
Ta có:
góc IKH = góc IHK ( định nghĩa hình thang cân NMHK)
mình bổ sung câu trả lời
Ta có:
góc IKH = góc IHK ( định nghĩa hình thang cân NMHK)
=> tam giác IKH cân tại I
Mà IO là đường phân giác cũng là đường cao
Nên IO vuông góc với HK (đpcm)