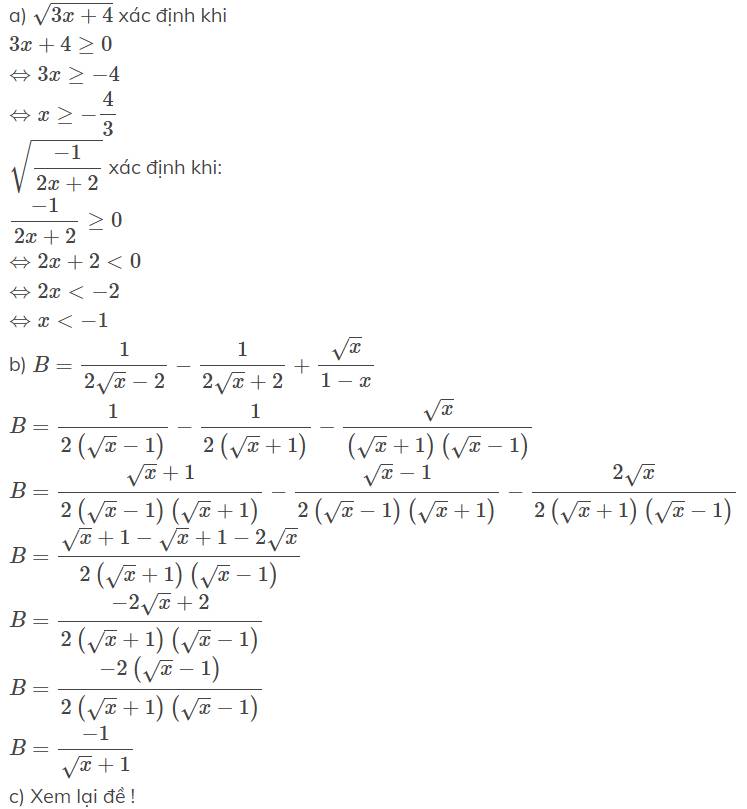Muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó

a) 

\(P=\left(\dfrac{b-a}{\sqrt{b}-\sqrt{a}}-\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}\right):\dfrac{\left(\sqrt{b}-\sqrt{a}\right)^2+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)

\(=\left[\sqrt{b}+\sqrt{a}-\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\right]:\dfrac{b-\sqrt{ab}+a}{\sqrt{a}+\sqrt{b}}\)

\(=\left(\sqrt{b}+\sqrt{a}-\dfrac{a+\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}\right).\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)

\(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2-a-\sqrt{ab}-b}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)

\(=\dfrac{\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)\(=\dfrac{\sqrt{ab}}{a-\sqrt{ab}+b}\)

b) \(P=\dfrac{\sqrt{ab}}{a-\sqrt{ab}+b}=\dfrac{\sqrt{ab}}{\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b}\)

Vì \(\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b>0;\forall a\ge0;b\ge0;a\ne b\)

\(\sqrt{ab}\ge0\)\(\forall a\ge0;b\ge0\)

\(\Rightarrow P=\dfrac{\sqrt{ab}}{\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b}\ge0\)

Vậy...

cảm ơn tất cả mọi người

a: \(=\dfrac{a+\sqrt{ab}-a+\sqrt{ab}-2b}{a-b}\)

\(=\dfrac{2\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a-b}\)

\(=\dfrac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)

a: \(=\dfrac{\sqrt{a}-1}{\sqrt{a}\left(a-\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{1}\)

\(=a-1\)

b: \(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}+\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}\right)\)

\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{\sqrt{ab}+b+\sqrt{ab}-b}{\sqrt{a}\left(a-b\right)}\)

\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{1}{\sqrt{a}}\)

c: \(=\dfrac{a\sqrt{b}+b}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2b\sqrt{ab}}{a^2+2a\sqrt{b}+b}}\cdot\left(\sqrt{a}+\sqrt{b}\right)\)

\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\sqrt{\dfrac{b\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(a+\sqrt{b}\right)^2}}\)

\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a+\sqrt{b}}=b\)

\(\sqrt{\dfrac{a}{b}}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}}=2\sqrt{\dfrac{a}{b}}\)

b) Ta có: \(4x^2+x-5=0\)

\(\Leftrightarrow4x^2-4x+5x-5=0\)

\(\Leftrightarrow4x\left(x-1\right)+5\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(4x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\4x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-\dfrac{5}{4}\left(loại\right)\end{matrix}\right.\)

Thay x=1 vào biểu thức \(B=\dfrac{\sqrt{x}-1}{\sqrt{x}}\), ta được:

\(B=\dfrac{\sqrt{1}-1}{\sqrt{1}}=0\)

Vậy: Khi \(4x^2+x-5=0\) thì B=0

a. \(=\dfrac{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}=\sqrt{a}\)

b. \(=\dfrac{1-\left(2\sqrt{a}\right)^3}{1-2\sqrt{a}}=\dfrac{\left(1-2\sqrt{a}\right)\left(1+2\sqrt{a}+4a\right)}{1-2\sqrt{a}}=1+2\sqrt{a}+4a\)

c. \(=\dfrac{1-\left(\sqrt{a}\right)^2}{1+\sqrt{a}}=\dfrac{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)}{1+\sqrt{a}}=1-\sqrt{a}\)

d. \(=\dfrac{\sqrt{a}\left(\sqrt{a}-3\right)}{\sqrt{a}-3}=\sqrt{a}\)

\(1,ĐKXĐ:x\ge0\\ x\sqrt{3}=-\sqrt{3x^2}\\ \Leftrightarrow3x^2=9x^2\\ \Leftrightarrow6x^2=0\\ \Leftrightarrow x=0\left(tm\right)\)

\(2,ab^2\sqrt{a}=ab^2\sqrt{a}\)

\(3,a\sqrt{\dfrac{b}{a}}=\sqrt{ab}\)

\(ab^2\sqrt{a}=\sqrt{a^3b^4}\)