Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác như hình 10.26 để có thể ghép được các mặt bên của hình chóp tứ giác đều.

Thực hành :
Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác theo thứ tự từ 1 đến 6 để có thể ghép được các mặt bên của một hình chóp tứ giác đều (h.122)
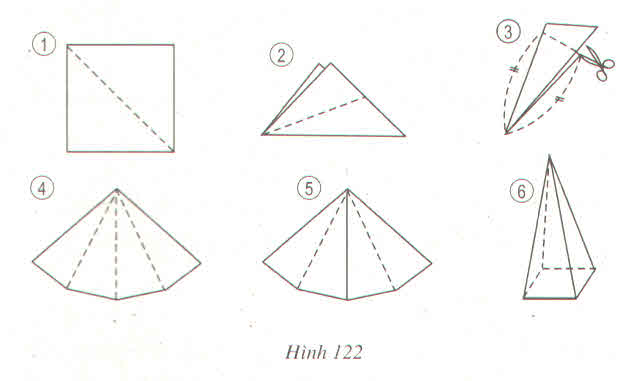
Người ta cắt một tờ giấy hình vuông có cạnh bằng 2 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
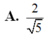
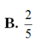
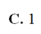
Người ta cắt một tờ giấy hình vuông có cạnh bằng 2 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
A. 2 5
B. 2 5
C. 1
D. 4 5
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
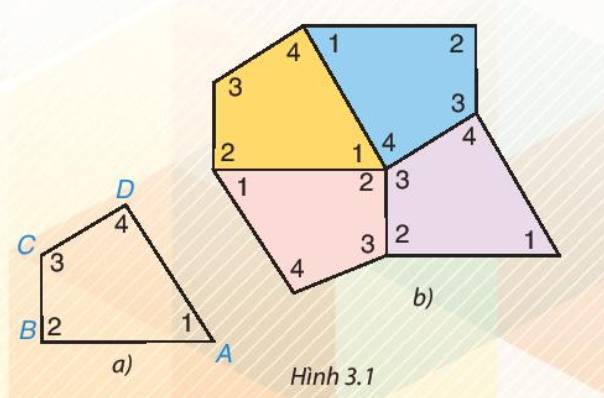
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.
- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Lấy một tờ giấy, gấp làm tư để có một góc vuông như triong Hình 16, dùng kéo cắt theo đường \(MN\) sao cho \(OM = ON\). Mở phần giấy cắt được ra ta được một tứ giác. Tứ giác đó là hình gì. Giải thích kết luận của em.
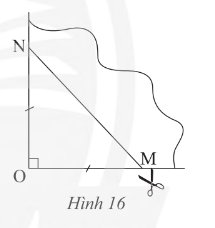
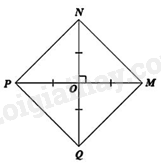
Vì \(OM = ON = OP = OQ\) nên \(O\) là trung điểm của \(NQ\) và \(MP\) và \(MP = NQ\)
Xét tứ giác \(MNPQ\) có hai đường chéo \(NQ\) và \(MP\) cắt nhau tại trung điểm \(O\) (cmt)
Suy ra \(MNPQ\) là hình bình hành
Mà \(MP = NQ\) (cmt) nên \(MNPQ\) là hình chữ nhật
Lại có \(MP \bot NQ\) (gt) nên \(MNPQ\) là hình vuông
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
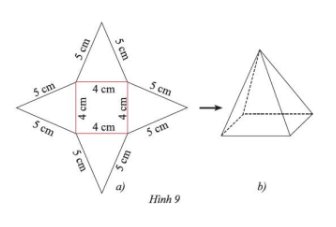
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.
Mai đánh dấu một số điểm trên tờ giấy màu (như hình vẽ). Qua hai điểm trong các điểm đã đánh dấu, Mai có thể cắt tờ giấy theo đoạn thẳng nào để được:
a) 2 hình tứ giác?
b) 1 hình tam giác và 1 hình tứ giác?
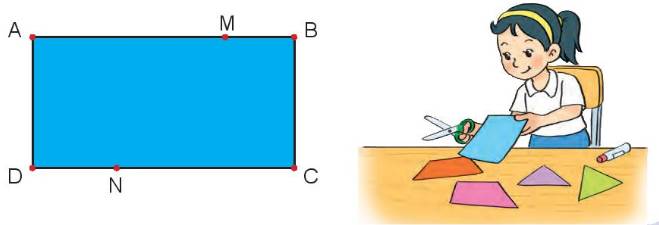
a) Mai cắt tờ giấy theo đoạn thẳng MN để có 2 hình tứ giác
b) Mai cắt tờ giấy theo những đoạn thẳng AN, BN, DM,CM để đc 1 hình tam giác và 1 hình tứ giác
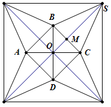
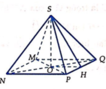
Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều (hình vẽ). Biết cạnh hình vuông bằng 20 (cm), OM = x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.
A. x = 9 (cm)
B. x = 8 (cm)
C. x = 6 (cm)
D. x = 7 (cm)
Đáp án B.
Sau khi cắt miếng giấy hình vuông như hình vẽ, ta xếp lại được thành hình chóp tứ giác đều S.MNPQ (hình bên).
 Ta có
O
M
=
x
⇒
M
P
=
M
Q
=
20
M
=
2
x
=
M
N
2
⇒
M
N
=
2
x
(cm).
Ta có
O
M
=
x
⇒
M
P
=
M
Q
=
20
M
=
2
x
=
M
N
2
⇒
M
N
=
2
x
(cm).
Gọi H là trung điểm P Q ⇒ O H = M N 2 = 2 x 2 (cm) và S H = 10 2 - 2 x 2 (cm).
Suy ra S O = S H 2 - O H 2 = 10 2 - 2 x 2 2 - 2 x 2 2 = 20 ( 10 - x ) .
Thể tích khối chóp S.MNPQ là:
V
M
N
P
Q
=
1
3
.
S
O
.
S
M
N
P
Q
=
1
3
20
(
10
-
x
)
.
2
x
2
=
20
3
(
40
-
4
x
)
.
x
4
→
V
M
N
P
Q
=
20
3
(
40
-
4
x
)
.
x
.
x
.
x
.
x
≤
20
3
40
-
4
x
+
x
+
x
+
x
+
x
5
=
256
10
3
Dấu “=” xảy ra ⇔ 40 - 4 x = x ⇔ x = 8 (cm).
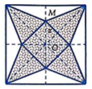
Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều (hình vẽ). Biết cạnh hình vuông bằng 20 (cm), OM=x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.
A. 9cm
B. 8cm
C. 6cm
D. 7cm