(ko cần vẽ hình, giải chi tiết)
Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E và F là các tiếp điểm). EF cắt OM và OA lần lượt tại H và K.
1) Chứng minh: H là trung điểm của EF.
2) Chứng minh rằng bốn điểm O, M, A, F cùng thuộc một đường tròn.
3) Chứng minh: \(OK.OA=R^2\)

Những câu hỏi liên quan
(ko cần vẽ hình, giải chi tiết)
Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E và F là các tiếp điểm). EF cắt OM và OA lần lượt tại H và K.
1) Chứng minh: H là trung điểm của EF.
2) Chứng minh rằng bốn điểm O, M, A, F cùng thuộc một đường tròn.
3) Chứng minh: OK.OAR^2
Đọc tiếp
(ko cần vẽ hình, giải chi tiết)
Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E và F là các tiếp điểm). EF cắt OM và OA lần lượt tại H và K.
1) Chứng minh: H là trung điểm của EF.
2) Chứng minh rằng bốn điểm O, M, A, F cùng thuộc một đường tròn.
3) Chứng minh: \(OK.OA=R^2\)
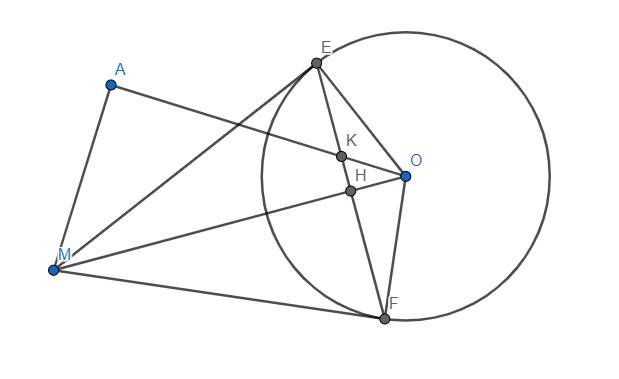
a) Ta thấy \(OE=OF\Rightarrow\) O thuộc trung trực của EF.
Mặt khác, theo tính chất của 2 tiếp tuyến cắt nhau, \(ME=MF\), suy ra M cũng nằm trên trung trực của EF.
\(\Rightarrow\)OM là trung trực của EF. Mà OM cắt EF tại H nên H là trung điểm EF (đpcm)
b) Ta thấy \(\widehat{OAM}+\widehat{OFM}=90^o+90^o=180^o\) nên tứ giác OAMF nội tiếp hay 4 điểm O, M, A, F cùng thuộc 1 đường tròn.
c) Vì OM là trung trực EF nên \(OM\perp EF\) tại H \(\Rightarrow\widehat{MHK}=90^o\)
Từ đó dễ thấy tứ giác AMHK nội tiếp \(\Rightarrow OA.OK=OH.OM\)
Mà \(OH.OM=OE^2=R^2\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow OA.OK=R^2\) (đpcm)
Đúng 1
Bình luận (0)
Ta có hai đường tròn (O ;2cm) và ( A ;2cm) cắt nhau tại C ,D .Điểm A nằm trên đường tròn tâm O .
a) Vẽ đường tròn tâm C , bán hính 2 cm
b) Vì sao đường tròn ( C;2cm) đi qua O ,A?
CÁC BẠN VẼ HÌNH VÀ GIẢI CHI TIẾT RA GIÚP MK VS .CÁC BẠN LÀM CÂU b) THÔI CŨNG ĐƯỢC VÀ GIẢI THÍCH CHO MK VS NHA! MK SẼ TICK.
Trên đoạn thẳng AB lấy điểm O và I sao cho OA<OB và AI > IB .Hỏi trong các bộ 3 điểm A,O,I và B,O,I điểm nào nằm giữa 2 điểm còn lại
( Ko cần vẽ hình, chỉ cần giải đúng,Ko cần chi tiết chỉ cần 100%)
O nằm giữa A và I
I nằm giữa O và B
Đúng 0
Bình luận (0)
Giải chi tiết giúp tớ với ah (ko cần vẽ hình cũng đc)
a) vì xoy+yoz=180 độ(2 góc kề bù)
=> yoz=180-xoy=130 độ
Đúng 0
Bình luận (0)
vì oa là tia phân giác của xoy
=> xoa=aoy=xoy/2=50/2=25độ
vì ob .................................yoz
=> yob=boz=yoz/2=130/2=65độ
=> aob=aoy+yob=25+65=90độ
Đúng 0
Bình luận (0)
Nếu đường kính hình tròn giảm đi 60% thì diện tích hình tròn giảm đi bao nhiêu % ?
Giải chi tiết hộ mik được ko a. !
- Coi đường kính hình tròn ban đầu là 100 (cm)
=> bán kính hình tròn ban đầu là: 100:2=50 (cm)
- Ta có công thức: S=π.r\(^2\)
=> diện tích hình tròn ban đầu là: 2500π (cm\(^2\))
- Đường kính hình tròn sau khi giảm là: 100- 100x60%=40 (cm)
=> bán kính hình tròn sau khi giảm là: 40:2=20 (cm)
- Ta có công thức: S=π.r\(^2\)
=> diện tích hình tròn sau khi giảm là: 400π (cm\(^2\))
=> diện tích hình tròn giảm đi: 2500π-400π=2100π (cm\(^2\))
=> diện tích hình tròn giảm đi: \(\dfrac{2100}{2500}\) x100%=84%
(Vì đây là toán lớp 5 nên cách làm như này mình nghĩ là dễ hiểu nhất rồi mặc dù có hơi dài dòng một chút :<< )
Đúng 1
Bình luận (0)
Làm chi tiết với ạ ( Vẽ hình luôn )Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyên với nửa đường tròn, cắt Ax và By lần lượt tại C và D . Khi đó MC . MD bằng A.OC^2 B.OM^2 C.OD^2 D.OM
Đọc tiếp
Làm chi tiết với ạ ( Vẽ hình luôn )
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyên với nửa đường tròn, cắt Ax và By lần lượt tại C và D . Khi đó MC . MD bằng
A.OC\(^2\) B.OM\(^2\) C.OD\(^2\) D.OM
cho đường tròn (o) đường kính AB vẽ đường tròn K tiếp xúc với đường tròn (o) tại C .Các dây CA ,CB cắt đường tròn (K) lần lượt tại E và F . CM rằng E K F thẳng hàng
mình cảm ơn các bạn nhiều lắm các bạn giải chi tiết hộ mình
Bạn tự vẽ hình nha :D
Xét đường tròn \(\left(O\right)\) có \(\widehat{ACB}=90^0\) nên:
\(\Rightarrow\widehat{ECF}=90^0\)
Xét đường tròn \(\left(K\right)\) vì \(\widehat{ECF}=90^0\) nên:
\(\Rightarrow EF\) là đường kính.
Từ những điều trên ta suy ra được \(E,K,F\) thẳng hàng (đpcm)
Cho ΔABC nội tiếp đường tròn ( O ) Các đường cap AM, BN cắt nhau tại H.
a) CM: Bốn điểm H, N, C, M cùng thuộc 1 đường tròn
b) CM: ANMB nội tiếp đường tròn
✳ Vẽ hình chi tiết giúp em với ạ
a: Xét tứ giác HMCN có
\(\widehat{HMC}+\widehat{HNC}=180^0\)
Do đó: HMCN là tứ giác nội tiếp
b: Xét tứ giác ANMB có
\(\widehat{ANB}=\widehat{AMB}=90^0\)
Do đó: ANMB là tứ giác nội tiếp
Đúng 0
Bình luận (0)
cho tam giác ABC(AB< AC) nội tiếp đường tròn (o) dường trung tuyến AM lấy điểm D trên cung BC không chứa A sao cho 2 góc BAD=CAM chúng minh rằng 2 góc ADB= CDM
các bạn khỏi vẽ hình nha các bạn chỉ cần giải ra cho mình là dc rồi nhung chi tiết hộ mình mình cảm ơn nhiều lắm





















