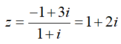Biểu diễn các điểm M(-1;-2), N(-2;-4), P(2;-3), Q(3;-4,5) trên hệ trục tọa độ Oxy. Tìm tọa độ các điểm M', N', P', Q' lần lượt đối xứng với M,N,P,Q qua Ox

Những câu hỏi liên quan
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ sau trên trục số: \( - 0,75;\,\frac{1}{{ - 4}};\,1\frac{1}{4}.\)
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)

Đúng 0
Bình luận (0)
Điểm P biểu diễn: \(-\dfrac{4}{3}\)
Điểm N biểu diễn: \(-\dfrac{1}{3}\)
Điểm M biểu diễn: \(\dfrac{5}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Kí hiệu S là tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện
z
−
1
+
i
z
+
2
i
và điểm A là điểm biểu diễn số phức 1+2i. Biết rằng
M
∈
S
là điểm sao cho AM nhỏ nhất. Tung độ của điểm M là giá trị nào sau đây? A.
M...
Đọc tiếp
Kí hiệu S là tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z − 1 + i = z + 2 i và điểm A là điểm biểu diễn số phức 1+2i. Biết rằng M ∈ S là điểm sao cho AM nhỏ nhất. Tung độ của điểm M là giá trị nào sau đây?
A. M − 1 ; 0
B. M 1 ; - 2
C. M − 1 ; 1
D. M 1 ; 1
Các điểm M, N, P lần lượt là điểm biểu diễn cho các số phức
z
1
4
i
i
-
1
;
z
2
1
-
i
1
+
2
i
;
...
Đọc tiếp
Các điểm M, N, P lần lượt là điểm biểu diễn cho các số phức z 1 = 4 i i - 1 ; z 2 = 1 - i 1 + 2 i ; z 3 = - 1 + 2 i . Hỏi tam giác MNP có đặc điểm gì?
A. Tam giác vuông
B. Tam giác cân
C. đáp án khác
D. Tam giác đều
Các điểm M, N, P lần lượt là điểm biểu diễn cho các số phức
z
1
4
i
i
-
1
,
z
2
1
-
i
1
+
2
i...
Đọc tiếp
Các điểm M, N, P lần lượt là điểm biểu diễn cho các số phức z 1 = 4 i i - 1 , z 2 = 1 - i 1 + 2 i , z 3 = - 1 + 2 i Hỏi tam giác MNP có đặc điểm gì?
A. Tam giác vuông
B. Tam giác cân
C. đáp án khác
D. Tam giác đều
Trên mặt phẳng phức, cho điểm A biểu diễn số phức
3
−
4
i
, điểm B biểu diễn số phức
-
1
-
2
i
. Gọi M là trung điểm của AB, N là điểm đối xứng với M qua trục hoành. Khi đó điểm N biểu diễn số phức nào sau đây? A.
z
1
+
3
i
B.
z
-
1
+
3
i
C.
z...
Đọc tiếp
Trên mặt phẳng phức, cho điểm A biểu diễn số phức 3 − 4 i , điểm B biểu diễn số phức - 1 - 2 i . Gọi M là trung điểm của AB, N là điểm đối xứng với M qua trục hoành. Khi đó điểm N biểu diễn số phức nào sau đây?
A. z = 1 + 3 i
B. z = - 1 + 3 i
C. z = - 1 - 3 i
D. z = 1 - 3 i
Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức
w
1
+
i
3
z
+
2
, trong đó
z
-
1
≤
2
. A. Hình tròn tâm
I
3
;
3
bá...
Đọc tiếp
Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức w = 1 + i 3 z + 2 , trong đó z - 1 ≤ 2 .
A. Hình tròn tâm I 3 ; 3 bán kính R = 4 .
B. Đường tròn tâm I 3 ; 3 bán kính R = 4 .
C. Hình tròn tâm I 3 ; 3 bán kính R = 8 .
D. Đường tròn tâm I 3 ; 3 bán kính R = 8 .
Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w − 2 1 + i 3 . Từ đó
z − 1 ≤ 2 ⇔ w − 2 1 + i 3 − 1 ≤ 2 ⇔ w − 3 − i 3 ≤ 2 1 + i 3 ⇔ w − 3 + i 3 ≤ 4
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x − 2 + y i 1 + i 3 = z
⇒ z − 1 = x − 2 + y i 1 + i 3 − 1 = x − 3 − y − 3 i 1 + i 3 ⇒ z − 1 = x − y 3 + i y − x 3 + 4 3 4
z − 1 ≤ 2 ⇒ x − y 3 2 + y − x 3 + 4 3 2 ≤ 8 ⇒ x − 3 2 + y − 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z − z 0 ≤ R ( z 0 , α ≠ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .
Đúng 0
Bình luận (0)
Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức
w
1
+
i
3
z
+
2
, trong đó
z
-
1
≤
2
. A. Hình tròn tâm I(
3
;
3
) bán kính
R
4
. B. Đường tròn tâm I(
3
;
3
)...
Đọc tiếp
Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức w = 1 + i 3 z + 2 , trong đó z - 1 ≤ 2 .
A. Hình tròn tâm I( 3 ; 3 ) bán kính R = 4 .
B. Đường tròn tâm I( 3 ; 3 ) R = 8 bán kính R = 4 .
C. Hình tròn tâm I( 3 ; 3 ) bán kính R = 8 .
D. Đường tròn tâm I( 3 ; 3 ) bán kính R = 8 .
Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w - 2 1 + i 3 . Từ đó
z - 1 ≤ 2 ⇔ w - 2 1 + i 3 - 1 ≤ 2 ⇔ w - 3 - i 3 ≤ 2 1 + i 3 ⇔ w - 3 + i 3 ≤ 4 .
Vậy tập hợp cần tìm là hình tròn tâm I( 3 ; 3 ) bán kính R = 4. Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x - 2 + y i 1 + i 3 = z
⇒ z - 1 = x - 2 + y i 1 + i 3 - 1 = x - 3 - y - 3 i 1 + i 3 ⇒ z - 1 = x - y 3 + i y - x 3 + 4 3 4
z - 1 ≤ 2 ⇒ x - y 3 2 + y - x 3 + 4 3 2 ≤ 8 ⇒ x - 3 2 + y - 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I( 3 ; 3 ) bán kính R = 4. Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z - z 0 ≤ R ( z 0 , α ≢ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .
Đúng 0
Bình luận (0)
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện:
z
¯
+
1
-
i
≤
1
A. Đường tròn tâm I(-1;-1), bán kính R 1. B. Hình tròn tâm I(1;-1), bán kính R 1. C. Hình tròn tâm I(-1;-1), bán kính R 1 (kể cả những điểm nằm trên đường tròn). D. Đường tròn tâm I(1;-1), bán kính R 1.
Đọc tiếp
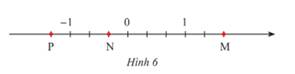
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: z ¯ + 1 - i ≤ 1
A. Đường tròn tâm I(-1;-1), bán kính R = 1.
B. Hình tròn tâm I(1;-1), bán kính R = 1.
C. Hình tròn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường tròn).
D. Đường tròn tâm I(1;-1), bán kính R = 1.
Chọn C.
Gọi M(x;y) là điểm biểu diễn của số phức z = x + yi trên mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có :
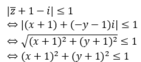
Suy ra, tập hợp các điểm M là hình tròn tâm I(-1;-1) bán kính R = 1 và kể cả đường tròn đó.
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
1
+
i
z
-
1
+
3
i
. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên? A. Điểm Q B. Điểm P C. Điểm M D. Điểm N
Đọc tiếp
Cho số phức z thỏa mãn 1 + i z = - 1 + 3 i .
Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên?
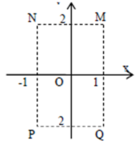
A. Điểm Q
B. Điểm P
C. Điểm M
D. Điểm N
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức
z
1
2
-
i
,
z
2
1
+
4
i
Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
Đọc tiếp
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức z 1 = 2 - i , z 2 = 1 + 4 i Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
![]()
![]()
![]()
![]()