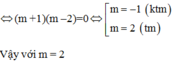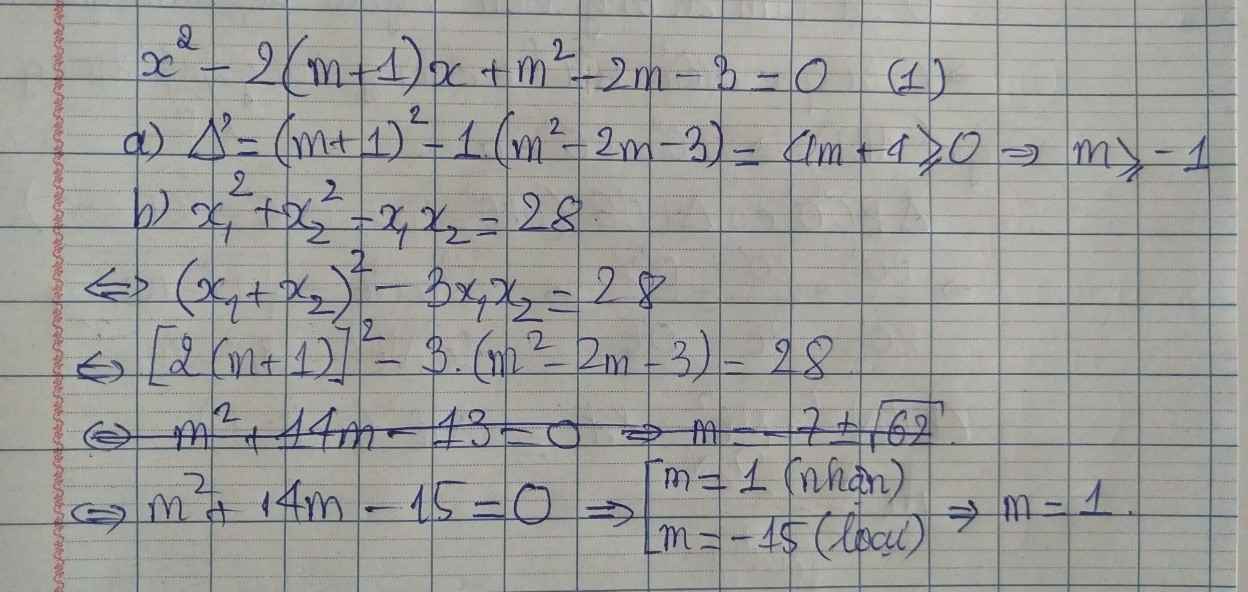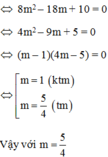cho pt x2 - 2(m+1)x + m2 - 1=0. Tìm để phương trình có hai nghiệm phân biệt thỏa mãn x12 + x22 = x1x2 +8

Những câu hỏi liên quan
Cho phương trình:
x
2
– 2(m – 1)x +
m
2
− 3m 0. Tìm m để phương trình có 2 nghiệm phân biệt
x
1
;
x
2
thỏa mãn
x
1
2
+
x
2
2
8
A. m 2 B....
Đọc tiếp
Cho phương trình: x 2 – 2(m – 1)x + m 2 − 3m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn x 1 2 + x 2 2 = 8
A. m = 2
B. m = −1
C. m = −2
D. m = 1
Cho phương trình
x
2
-
2
m
+
1
x
+
2
m
2
-
2
0
Tìm giá trị của m để phương trình có hai nghiệm phân biệt
x
1
;
x
2
thỏa mãn biểu thức A
x
1...
Đọc tiếp
Cho phương trình x 2 - 2 m + 1 x + 2 m 2 - 2 = 0 Tìm giá trị của m để phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn biểu thức A = x 1 2 + x 2 2 + x 1 x 2 đạt giá trị nhỏ nhất.
A. m=1
B. Không tồn tại m.
C. m=-2
D. Có vô số giá trị m.
Cho phương trình ẩnx: x2–2(m+1)x+m2–2m–3=0(1)
a) Tìm m để phương trình (1) luôn có nghiệm .
b) Tìm giá trị của m để hai nghiệm x1; x2 của phương trình (1) thỏa hệ thức: x12 + x22 – x1x2 = 28
a: \(\Delta=\left(2m+2\right)^2-4\left(m^2-2m-3\right)\)
\(=4m^2+8m+4-4m^2+8m+12\)
=16m+16
Để phương trình luôn có nghiệm thì 16m+16>=0
hay m>=-1
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=28\)
\(\Leftrightarrow\left(2m+2\right)^2-3\left(m^2-2m-3\right)=28\)
\(\Leftrightarrow4m^2+8m+4-3m^2+6m+9=28\)
\(\Leftrightarrow m^2+14m-15=0\)
=>(m+15)(m-1)=0
=>m=1
Đúng 1
Bình luận (0)
Cho phương trình (ẩn x) : x 2 – 2mx – 4m – 4 = 0(1)
b) Tìm m để phương trình (1) có 2 nghiệm x 1 , x 2 thỏa mãn x 1 2 + x 2 2 - x 1 x 2 = 13 = 13
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
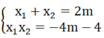
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
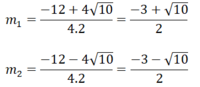
Vậy với 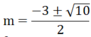 thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
Đúng 0
Bình luận (0)
Cho phương trình: x2 - 3x - m2 + m + 2 = 0 (1)
Tìm m để pt(1) có 2 nghiệm phân biệt x1,x2 sao cho: x12 + x22 = 5
\(\Delta=9-4\left(-m^2+m+2\right)=4m^2-4m+1=\left(2m-1\right)^2\)
Pt có 2 nghiệm pb khi \(m\ne\dfrac{1}{2}\)
Do vai trò của 2 nghiệm là như nhau, giả sử: \(\left\{{}\begin{matrix}x_1=\dfrac{3-\left(2m-1\right)}{2}=2-m\\x_2=\dfrac{3+2m-1}{2}=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\Leftrightarrow\left(2-m\right)^2+\left(m+1\right)^2=5\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình bậc hai x2 -2(m-1)x+m2 -3m-4(mlà tham số, xlà ẩn số).a) Tìm để phương trình có hai nghiệm phân biệt . b) Đặt A X12 + X22 -X1X2 Tính A theo m và tìm m để A18
Đọc tiếp
Cho phương trình bậc hai x2 -2(m-1)x+m2 -3m-4(mlà tham số, xlà ẩn số).
a) Tìm ![]() để phương trình có hai nghiệm phân biệt
để phương trình có hai nghiệm phân biệt ![]() .
.
b) Đặt A= X12 + X22 -X1X2 Tính A theo m và tìm m để A=18
a: Δ=(2m-2)^2-4(m^2-3m-4)
=4m^2-8m+4-4m^2+12m+16
=4m+20
Để phương trình có hai nghiệm phân biệt thì 4m+20>0
=>m>-20
b: A=(x1+x2)^2-3x1x2
=(2m-2)^2-3(m^2-3m-4)
=4m^2-8m+4-3m^2+9m+12
=m^2+m+16
Để A=18 thì m^2+m+16=18
=>m^2+m-2=0
=>(m+2)(m-1)=0
=>m=1 hoặc m=-2
Đúng 1
Bình luận (0)
Cho phương trình ẩn x: x2 - 2(m+1)x + m2 - 1 = 0 . Tìm giá trị của m để phương tình có 2 nghiệm x1 x2 thỏa mãn x12 + x22 = x1.x2 + 8
Lời giải:
Để PT có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m+1)^2-(m^2-1)>0\Leftrightarrow 2m+2>0\Leftrightarrow m>-1$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$ và $x_1x_2=m^2-1$
Khi đó, để $x_1^2+x_2^2=x_1x_2+8$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=x_1x_2+8$
$\Leftrightarrow (x_1+x_2)^2=3x_1x_2+8$
$\Leftrightarrow 4(m+1)^2=3(m^2-1)+8$
$\Leftrightarrow m^2+8m-1=0$
$\Leftrightarrow m=-4\pm \sqrt{17}$. Vì $m>-1$ nên $m=-4+\sqrt{17}$
Đúng 2
Bình luận (0)
Cho phương trình:
x
2
– 2mx + 2m – 1 0. Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn
2
(
x
1
2
+
x
2
2
)
−
5
x
1
.
x
2
−
1
A. m...
Đọc tiếp
Cho phương trình: x 2 – 2mx + 2m – 1 = 0. Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn 2 ( x 1 2 + x 2 2 ) − 5 x 1 . x 2 = − 1
A. m = 1
B. m = 5 4
C. m = −4
D. m = - 7 4
Cho phương trình ẩn x: x2 – 2mx - 1 = 0 (1)
a) Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt x1 và x2.
b) Tìm các giá trị của m để: x12 + x22 – x1x2 = 7
a, \(\Delta'=\left(-m\right)^2-1\left(-1\right)=m^2+1>0\)
Vậy phương trình đã cho luôn có hai nghiệm phân biệt x1 và x2
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
\(x^2_1+x^2_2-x_1x_2=7\\ \Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=7\\ \Leftrightarrow\left(2m\right)^2-3\left(-1\right)=7\\ \Leftrightarrow4m^2+3=7\\ \Leftrightarrow4m^2=4\\ \Leftrightarrow m^2=1\\ \Leftrightarrow m=\pm1\)
Đúng 0
Bình luận (0)