kẻ hình giúp mình nha

Cho hình thang cân MNPQ ( MN//PQ ,MN<PQ ).Kẻ các đường cao MA và NB của hình thang.Cm AQ = BP,và BQ=AP
mn giúp mình với nha mình đang cần gấp ( nhớ vẽ hình nha )
Xét ΔMAQ vuông tại A và ΔNBP vuông tại B có
MQ=NP
góc Q=góc P
=>ΔMAQ=ΔNBP
=>AQ=BP
=>AQ+AB=BP+BA
=>BQ=AP
Giúp mình nha,kẻ hình và giải theo cách lớp 9 ( chi tiết thì càng tốt ạ :>)
Mơn mn nhìu<33

d.
Ta có: \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(OB=OC=R\)
\(\Rightarrow OA\) là trung trực BC hay OA vuông góc BC tại I
Xét hai tam giác vuông AIB và ABO có:
\(\left\{{}\begin{matrix}\widehat{AIB}=\widehat{ABO}=90^0\\\widehat{BAI}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIB\sim\Delta ABO\left(g.g\right)\)
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{AB}{AO}\Rightarrow AI.AO=AB^2\)
Theo c/m câu c có \(AB^2=AE.AF\)
\(\Rightarrow AI.AO=AE.AF\)
e.
Từ đẳng thức trên ta suy ra: \(\dfrac{AI}{AF}=\dfrac{AE}{AO}\)
Xét hai tam giác AIE và AFO có:
\(\left\{{}\begin{matrix}\dfrac{AI}{AF}=\dfrac{AE}{AO}\left(cmt\right)\\\widehat{OAF}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIE\sim\Delta AFO\left(c.g.c\right)\)
\(\Rightarrow\widehat{AFO}=\widehat{AIE}\)
Mà \(\widehat{AIE}+\widehat{OIE}=180^0\) (kề bù)
\(\Rightarrow\widehat{AFO}+\widehat{OIE}=180^0\)
\(\Rightarrow\) Tứ giác FOIE nội tiếp
a.
Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\widehat{ABO}=90^0\)
\(\Rightarrow\) 3 điểm A, B, O thuộc đường tròn đường kính OA (1)
Tương tự AC là tiếp tuyến của (O) nên 3 điểm A, C, O thuộc đường tròn đường kính OA
\(\Rightarrow\) 4 điểm A, B, C, O thuộc đường tròn đường kính OA hay tứ giác ABOC nội tiếp
b.
Do M là trung điểm EF \(\Rightarrow OM\perp EF\Rightarrow\widehat{OMA}=90^0\)
\(\Rightarrow\) 3 điểm A, M, O thuộc đường tròn đường kính OA (2)
(1);(2) \(\Rightarrow\) 4 điểm A, B, M, O thuộc đường tròn đường kính OA
Hay tứ giác ABMO nội tiếp
c.
Xét hai tam giác ABE và AFB có:
\(\left\{{}\begin{matrix}\widehat{EAB}\text{ chung}\\\widehat{ABE}=\widehat{AFB}\left(\text{cùng chắn BE}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABE\sim\Delta AFB\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AE}{AB}\) \(\Rightarrow AB^2=AE.AF\)
CHO 1 TAM, GIÁC .HÃY DÙNG CÁC ĐƯỜNG THẲNG CHIA TAM GIÁC THÀNH 2 HÌNH SAO CHO SIỆN TÍCH NÀY GẤP 3 DIỆN TÍCH KUA
KẺ HÌNH GIẢI GIÚP MÌNH NHA MAI MÌNH NỘP
cho 1 tam giác hãy dùng các đường thẳng chia tam giác đó thành 2 hình sao cho diện tích này gấp 3 diện tích kia
Cho hình thang cân ABCD (AB // CD). Cho biết AB = 10cm, CD = 30cm,
BC = 13cm. Kẻ AH vuông góc với CD.
a) Tính diện tích hình thang ABCD.
b) Tính diện tích tứ giác ABHD.
Giúp mình nha
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. Chứng minh: AB2 + CH2 = AC2 + BH2
Mọi người giúp mình bài này với nha,mình cảm ơn nhiều!
(Mọi người không cần vẽ hình đâu ạ!)
\(AB^2=AH^2+BH^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\left(Pitago\right)\)
\(AC^2=AH^2+CH^2\Rightarrow AH^2=AC^2-CH^2\left(2\right)\left(Pitago\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AC^2-CH^2=AB^2-BH^2\)
\(\Rightarrow AB^2+CH^2=AC^2+BH^2\)
\(\Rightarrow dpcm\)
Ta có \(AB^2-AC^2=\left(BH^2+AH^2\right)-\left(CH^2+AH^2\right)\) \(=BH^2-CH^2\) \(\Rightarrow AB^2+CH^2=AC^2+BH^2\), đpcm.
(Bài này kết quả vẫn đúng nếu không có điều kiện tam giác ABC vuông tại A.)
 giúp kẻ hình nha :'>
giúp kẻ hình nha :'>
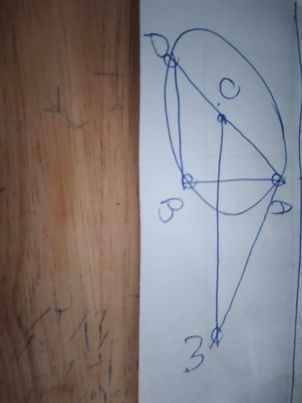
a: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
=>OAMB là tứ giác nội tiếp
=>O,A,M,B cùng thuộc một đường tròn
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM⊥AB(1)
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó:ΔABD vuông tại B
=>AB⊥BD(2)
Từ (1) và (2) suy ra OM//BD
kẻ hình giúo mình nha

3:
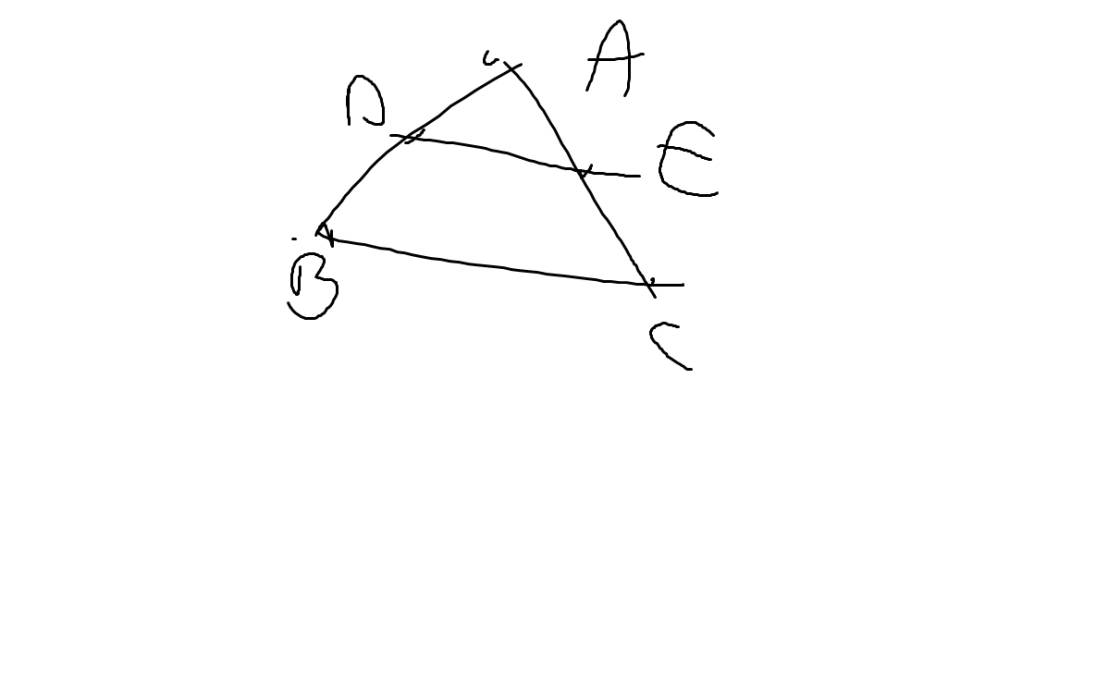
a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Xét tứ giác BDEC có
DE//BC
góc B=góc C
=>BDEC là hình thang cân
b: góc ABC=góc ACB=(180-góc A)/2
=(180-50)/2=65 độ
=>góc BDE=góc DEC=180-65=115 độ
tam giác abc cân tại a. kẻ đường cao BH, CK
a) CM tam giác BHC = tam giác BKC
b) CM AH=AK
c) Tứ giác BKHC là hình gì?Vì sao?
GIÚP MÌNH NHA, MÌNH BỊ NGU HÌNH HỌC

kẻ hộ mình cái hình nha