Các mặt của một hình lập phương là các hình gì? Vì sao?

Những câu hỏi liên quan
Cho mặt nón có chiều cao h 6 bán kính đáy r 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
Đọc tiếp
Cho mặt nón có chiều cao h = 6 bán kính đáy r = 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
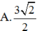
![]()
![]()
![]()
Cho mặt nón có chiều cao h 6 bán kính đáy r 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương. A.
3
2
2
B.
6
2
-
1...
Đọc tiếp
Cho mặt nón có chiều cao h = 6 bán kính đáy r = 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
A. 3 2 2
B. 6 2 - 1
C. 3 2 + 3
D. 3
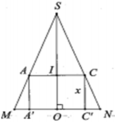
Cho mặt nón có chiều cao h 6, bán kính đáy r 3. Hình lập phương ABCD.A’B’C’D’ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng A.
3
3
B.
3
6
2
C. ...
Đọc tiếp
Cho mặt nón có chiều cao h = 6, bán kính đáy r = 3. Hình lập phương ABCD.A’B’C’D’ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng
A. 3 3
B. 3 6 2
C. 6 3 2 - 1
D. 6 2 - 1
Đáp án A
Phương pháp:
Cắt khối hình bởi mặt phẳng đi qua trục
Tính độ dài x cạnh của hình lập phương
Tính độ dài đường chéo của hình lập phương: x 3
Cách giải:
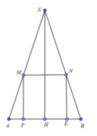
Xét mặt cắt qua trục có SH = h = 6, HA = HB = r = 3
Gọi độ dài cạnh của hình vuông là x.
![]()
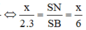
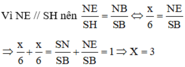
=> Độ dài đường chéo của hình lập phương là: 3 3
Đúng 0
Bình luận (0)
một hình lập phương có các mặt được viết các số từ 1 đến 6 sao cho tổng các số trên các mặt đối diện bằng 7. hình lập phương này được đặt trên một mặt bàn phẳng . người ta xoay hình lập phương dó sao cho cạnh PQ lên phía trên sau đó lại xoay hình lập phương đó sao cho cạnh PR lên phía trên.hỏi số ghi ở mặt trên cùng khi đó là số nào
Quan sát hình lập phương ABCD. A’B’C’D’ ở Hình 10 và thực hiện các hoạt động sau:
a) Mặt AA’D’D là hình gì?
b) So sánh độ dài các cạnh của hình lập phương đó.
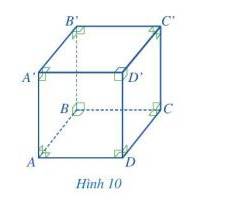
a) Mặt AA’D’D là hình gì vuông
b) Các cạnh của hình lập phương đó bằng nhau
Đúng 0
Bình luận (0)
a) Có thể xếp 343 hình lập phương đơn vị (cạnh dài 1 đơn vị) thành 1 hình lập phương không? Vì sao?b) Muốn được 1 hình lập phương cạnh dài 10 đơn vị thì phải có thêm bao nhiêu hình lập phương đơn vị nữa?c) Nếu sơn tất cả các mặt của hình lập phương cạnh dài 10 đơn vị nói trên thì trong các hình lập phương đơn vị, có bao nhiêu hình lập phương mà:+ Có 3 mặt được sơn?+ Có đúng 2 mặt được sơn?+ Chỉ có 1 mặt được sơn?
Đọc tiếp
a) Có thể xếp 343 hình lập phương đơn vị (cạnh dài 1 đơn vị) thành 1 hình lập phương không? Vì sao?
b) Muốn được 1 hình lập phương cạnh dài 10 đơn vị thì phải có thêm bao nhiêu hình lập phương đơn vị nữa?
c) Nếu sơn tất cả các mặt của hình lập phương cạnh dài 10 đơn vị nói trên thì trong các hình lập phương đơn vị, có bao nhiêu hình lập phương mà:
+ Có 3 mặt được sơn?
+ Có đúng 2 mặt được sơn?
+ Chỉ có 1 mặt được sơn?
Một hình lập phương có cạnh 4cm. Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh 1cm. Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ? A. 16 B. 48 C. 8 D. 24
Đọc tiếp
Một hình lập phương có cạnh 4cm. Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh 1cm. Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ?
A. 16
B. 48
C. 8
D. 24
Chọn D
Mỗi mặt của khối lập phương chứa 4 mặt của 4 khối lập phương nhỏ chỉ có 1 mặt được sơn đỏ Vậy số khối lập phương chỉ có 1 mặt được sơn đỏ là 4x6=24.
Đúng 0
Bình luận (0)
Một hình lập phương có cạnh 4 cm. Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh 1 cm. Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ?
A. 8
B. 16
C. 24
D. 48
Đáp án C.
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu.

Đúng 0
Bình luận (0)
Một hình lập phương có cạnh 4cm. Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh 1cm. Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ? A. 8. B. 16 C. 24 D. 48
Đọc tiếp
Một hình lập phương có cạnh 4cm. Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh 1cm. Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ?
A. 8.
B. 16
C. 24
D. 48