Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.

Những câu hỏi liên quan
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.
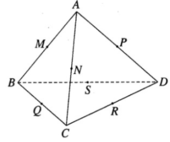
Giả sử có một mặt cầu tiếp xúc với các cạnh AB, AC, AD, BC, CD, BD của tứ diện ABCD lần lượt tại M, N, P, Q, R, S. Khi đó AM, AN, AP là các tiếp tuyến cùng xuất phát từ A nên AM = AN = AP.
Lập luận tương tự ta có: BM = BQ = BS; CQ = CR = CN; DR = DS = DP
Vậy AB + CD = AM + MB + CR + RD = AN + BS + CN + DS = AN + NC + BS + SD = AC + BD
Bằng lí luận tương tự ta chứng minh được AB + CD = AC + BD = AD + BC
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện có tổng các cặp cạnh đối diện bằng nhau ?
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng các cặp cạnh đối diện của tứ diện bằng nhau.
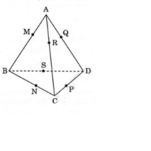
Gọi mặt cầu S(O; R) tiếp xúc với các cạnh của hình tứ diện đã cho lần lượt tại M, N, P, Q ,R và S.
* Ta chứng minh: AM = AR = AQ.
Do mặt cầu tiếp xúc với ba cạnh AB, AC và AD lần lượt tại M; R và Q nên :
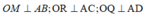
Xét ba tam giác OAM; OAR và OAQ có:
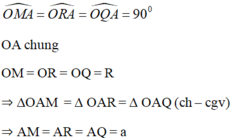
* Chứng minh tương tự ta có:
BM = BN = BS = b
CP = CN = CR = c.
DP = DQ = DS = d
Ta có:
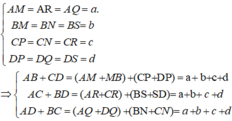
Do đó, AB + CD = AC + BD = AD + BC.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau
Gọi I và J lần lượt là trung điểm của AB và CD. Vì ΔACD = ΔBDC nên các tiếp tuyến tương ứng của chúng bằng nhau, do đó AJ = BJ. Từ đó suy ra IJ ⊥ AB. Tương tự, IJ ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
Làm tương tự đối với các cặp cạnh đối diện khác ta chứng minh được rằng đường nối trung điểm của các cặp cạnh đối diện là đường vuông góc chung của cặp cạnh đó. Do đó các đường đó đồng quy tại O là trung điểm của mỗi đường.
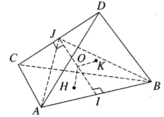
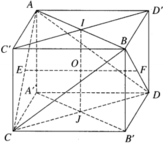
Gọi (P) là mặt phẳng qua AB và song song với CD, (Q) là mặt phẳng qua CD và song song với AB; A', B' lần lượt là hình chiếu vuông góc của A, B lên (Q); C', D' lần lượt là hình chiếu vuông góc của C, D lên (P). Dễ thấy AC'BD'.A'CB'D là hình hộp chữ nhật. Đường nối hai tâm của mỗi cặp mặt đối diện của hình hộp chữ nhật đó chính là đường vuông góc chung của các cặp cạnh đối diện của tứ diện ABCD. Do đó chúng đôi một vuông góc với nhau.
Đúng 1
Bình luận (0)
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng độ dài của các cặp cạnh đối diện của tứ diện bằng nhau ?
Cho hình tứ diện ABCD. Từ hệ thức trên hãy suy ra định lí: “Nếu một hình tứ diện có hai cặp cạnh đối diện vuông góc với nhau thì cặp cạnh đối diện thứ ba cũng vuông góc với nhau.”
Từ hệ thức trên ta suy ra định lí: “Nếu tứ diện ABCD có AB ⊥ CD, AC ⊥ DB, nghĩa là AB → . C D → = 0 và AC → . D B → = 0 thì AD → . B C → = 0 và do đó AD ⊥ BC.”
Đúng 0
Bình luận (0)
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng
2
k
3
12
. Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng
a
2
. Tính theo a thể tích khối tứ diện
A
C
B
D...
Đọc tiếp
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
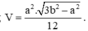
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là ![]()
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
![]()
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là
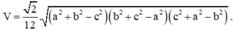
Đúng 0
Bình luận (0)
Cho hình tứ diện ABCD
a) Chứng minh hệ thức : \(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\)
b) Từ hệ thức hãy suy ra định lí :
"Nếu một hình tứ diện có hai cặp cạnh đối diện vuông góc với nhau thì cặp cạnh đối diện tứ ba cũng vuông góc với nhau"












