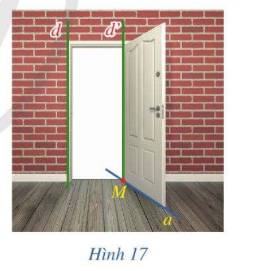
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d, a, b; sàn nhà coi như mặt phẳng (P) chứa a và b. Hỏi đường thẳng d có vuông góc với mặt phẳng (P) hay không?
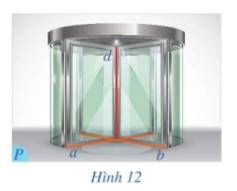
Hình 17 mô tả một cửa gỗ có dạng hình chữ nhật, ở đó nẹp cửa và mép dưới cửa lần lượt gợi nên hình ảnh hai đường thẳng d và a. Điểm M là vị trí giao giữa mép gắn bản lề và mép dưới của cửa. Hãy giải thích tại sao khi quay cánh cửa, mép dưới cửa là những đường thẳng a luôn nằm trên mặt phẳng đi qua điểm M cố định và vuông góc với đường thẳng d.
Tham khảo
Vì sàn nhà là một mặt phẳng vuông góc với đường thẳng d. Mà đường thẳng a luôn nằm trên mặt phẳng đó nên đường thẳng d luôn vuông góc với đường thẳng a
Hình 17 mô tả một cửa gỗ có dạng hình chữ nhật, ở đó nẹp cửa và mép dưới cửa lần lượt gợi nên hình ảnh hai đường thẳng d và a. Điểm M là vị trí giao giữa mép gắn bản lề và mép dưới của cửa. Hãy giải thích tại sao khi quay cánh cửa, mép dưới cửa là những đường thẳng a luôn nằm trên mặt phẳng đi qua điểm M cố định và vuông góc với đường thẳng d.

a) Giao tuyến ∆ của hai mặt phẳng (Q), (R) có vuông góc với mặt phẳng (P) hay không?
b) Có bao nhiêu đường thẳng đi qua O và vuông góc với (P)?
a: \(a\perp\left(Q\right);\Delta\subset\left(Q\right)\)
=>\(\Delta\perp a\)(1)
\(b\perp\left(R\right);\Delta\subset\left(R\right)\)
=>\(\Delta\perp b\)(2)
mà a,b thuộc (P)(3)
nên từ (1), (2), (3) suy ra \(\Delta\perp\left(P\right)\)
b: Có 1 đường duy nhất
Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng \(a\) và \(b\) chéo nhau, hai bản lề của cánh cửa nằm trên đường thẳng \(c\).
Quan sát Hình 73 và cho biết đường thẳng \(c\) có vừa cắt, vừa vuông góc với cả hai đường thẳng \(a\) và \(b\) hay không.

c vừa cắt, vừa vuông góc với a,b
Nền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) và đường thẳng \(a\) nằm trên mặt phẳng \(\left( P \right)\). Quan sát Hình 48 và cho biết:
a) Vị trí tương đối của đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\);
b) Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có vuông góc với nhau không.
a: \(a\perp\left(Q\right)\)
b: Hai mặt phẳng (P) và (Q) có vuông góc với nhau
Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới của lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.
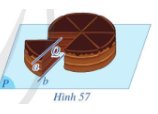
Hai đường thẳng a, b có song song với nhau vì a song song với (P) mà (Q) cắt (P) tại giao tuyến b.
Hình 78 mô tả bóng nắng của một lan can cầu đường bộ trên mặt đường, tức là hình chiếu của lan can qua phép chiếu song song lên mặt đường. Thanh lan can gợi nên hình ảnh đường thẳng nối các điểm A, B, C, ở đó B nằm giữa A và C. Gọi các điểm A’, B’, C’ lần lượt là bóng nắng của các điểm A, B, C trên mặt đường.

Quan sát Hình 78 và cho biết:
a) Các điểm A’, B’, C’ có thẳng hàng hay không. Nếu có, điểm B’ có nằm giữa hai điểm A’ và C’ hay không’
b) Bóng nắng của thanh lan can là hình gì.
a) Quan sát Hình 78, ta thấy các điểm A’, B’, C’ thẳng hàng và điểm B’ nằm giữa hai điểm A’, C’.
b) Bóng nắng của thanh lan can là đường thẳng.
Trong Hình 56, hai mặt tường của căn phòng gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến b, mép cột gợi nên hình ảnh đường thẳng a. Cho biết đường thẳng a có song song với giao tuyến b hay không.
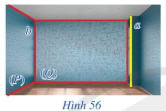
a) • Ta có: M ∈ b và (P) ∩ (Q) = b;
Suy ra M ∈ (P).
Mà M ∈ (M, a)
Do đó M là giao điểm của (P) và (M, a).
Lại có b’ = (P) ∩ (M, a)
Suy ra đường thẳng b’ đi qua M.
Tương tự ta cũng chứng minh được b’’ đi qua điểm M.
• Ta có: a // (P);
a ⊂ (M, a)
(M, a) ∩ (P) = b’
Do đó a // b’.
Tương tự ta cũng có a // b’’.
Do đó b’ // b’’.
Mặt khác: (P) ∩ (Q) = b;
(M, a) ∩ (P) = b’;
(M, a) ∩ (Q) = b’’;
b // b’’.
Do đó b // b’ // b’’.
Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.
b) Vì a // b’ nên a // b (do b ≡ b’).
tham khảo
Ta có:\(a//\left(P\right)\)
\(a//\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=b\)
Do đó theo hệ quả định lí \(2\) ta có \(a//b\).
Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà. Coi dây dọi như đường thẳng d và nền nhà như mặt phẳng (P), khi đó Hình 10 gợi nên hình ảnh đường thẳng d vuông góc với mặt phẳng (P). Người thợ xây đặt chiếc thước thẳng ở một vị trí tùy ý trên nền nhà. Coi chiếc thước thẳng đó là đường thẳng a trong mặt phẳng (P), nêu dự đoán về mối liên hệ giữa đường thẳng d và đường thẳng a.
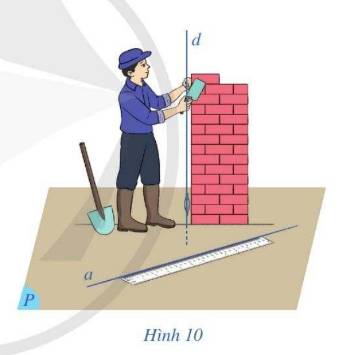
Đường thẳng d và đường thẳng a vuông góc với nhau
Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau và cách nhau một khoảng d; khi cửa đóng, hai đường kính đó trùng nhau. Hãy tính số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm.

Gọi đường kính của khung là AB có tâm I và đường kính của cánh là MN có tâm I’
=> II’ = d = 40cm
Vì đường kính của khung và đường kính của cánh song song với nhau nên mặt phẳng chứa cánh song song với mặt phẳng chứa khung
=> Hai mặt phẳng đó cắt nhau tại 1 đường thẳng d’ qua O song song với AB và MN.
Vì O là điểm chính giữa nên \(OI \bot AB,OI' \bot MN\)
=> \(d' \bot OI,d' \bot OI'\)
Do đó góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa là góc \(\widehat {IOI'}\)
Xét tam giác IOI’ có
\(OI = OI' = \frac{{80}}{2} = 40 \Rightarrow OI = OI' = II'\)
\( \Rightarrow \) Tam giác IOI’ đều \( \Rightarrow \) \(\widehat {IOI'} = {60^0}\)
Vậy số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm là 600