c vừa cắt, vừa vuông góc với a,b
Bài 5. Khoảng cách
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song Delta và Delta . Xét điểm A trên đường thẳng Delta .a) Khoảng cách từ điểm A đến đường thẳng Delta có phụ thuộc vào vị trí của điểm A trên đường thẳng Delta hay không? Vì sao?b) Khoảng cách đó gợi nên khái niệm gì trong hình học liên quan đến hai đường thẳng song song Delta và Delta ?
Đọc tiếp
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song \(\Delta \) và \(\Delta '\). Xét điểm \(A\) trên đường thẳng \(\Delta \).
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(\Delta '\) có phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \) hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm gì trong hình học liên quan đến hai đường thẳng song song \(\Delta \) và \(\Delta '\)?
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng Delta và mặt phẳng left( P right) song song với nhau, chiều cao của chiếc cột có đỉnh cột A là khoảng cách từ điểm A đến mặt phẳng left( P right).a) Khoảng cách từ điểm A đến mặt phẳng left( P right) có phụ thuộc vào vị trí của điểm A trên đường thẳng Delta hay không? Vì sao?b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng Delta và mặt phẳng left( P right)?
Đọc tiếp
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\) song song với nhau, chiều cao của chiếc cột có đỉnh cột \(A\) là khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\).
a) Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\) có phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \) hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)?
Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m. Tại sao có thể nói khoảng cách giữa hai cột đèn đó là 5 m.
Cho hình lăng trụ \(ABC.A'B'C'\) có cạnh bên bằng \(a\), góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^ \circ }\). Tính khoảng cách giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\).
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí \(M\) trên tường có độ cao so với nền nhà là \(MH = 80cm\). Quan sát Hình 61, nền nhà gợi nên mặt phẳng \(\left( P \right)\), cho biết độ dài đoạn thẳng \(MH\) gợi nên khái niệm gì trong hình học liên quan đến điểm \(M\) và mặt phẳng \(\left( P \right)\).
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song left( P right),left( Q right). Chiều cao của căn phòng là 3 m.Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song left( P right),left( Q right)?b) Cho hai mặt phẳng left( P right) và left( Q right) song song với nhau. Xét điểm I tuỳ ý trong mặt phẳng left( P right), lấy K là hình chiếu của I trên left( Q right) (Hình 71). Khoảng cách IK từ điểm I đến mặt phẳng left( Q...
Đọc tiếp
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song \(\left( P \right),\left( Q \right)\). Chiều cao của căn phòng là 3 m.
Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song \(\left( P \right),\left( Q \right)\)?
b) Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Xét điểm \(I\) tuỳ ý trong mặt phẳng \(\left( P \right)\), lấy \(K\) là hình chiếu của \(I\) trên \(\left( Q \right)\) (Hình 71). Khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) có phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\) hay không? Vì sao?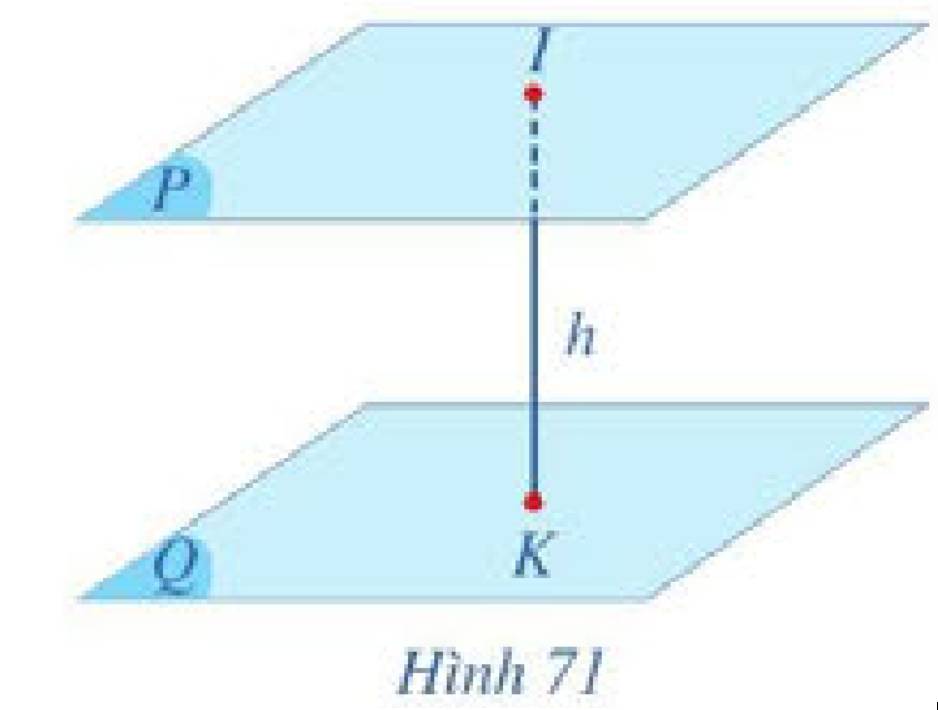
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
Với giả thiết ở Bài tập 2, hãy:a) Chứng minh rằng MNparallel BC. Tính khoảng cách giữa hai đường thẳng MN và BC.b) Chứng minh rằng MPparallel left( {BCD} right). Tính khoảng cách từ đường thẳng MP đến mặt phẳng left( {BCD} right).c) Chứng minh rằng left( {MNP} right)parallel left( {BCD} right). Tính khoảng cách giữa hai mặt phẳng left( {MNP} right) và left( {BCD} right).
Đọc tiếp
Với giả thiết ở Bài tập 2, hãy:
a) Chứng minh rằng \(MN\parallel BC\). Tính khoảng cách giữa hai đường thẳng \(MN\) và \(BC\).
b) Chứng minh rằng \(MP\parallel \left( {BCD} \right)\). Tính khoảng cách từ đường thẳng \(MP\) đến mặt phẳng \(\left( {BCD} \right)\).
c) Chứng minh rằng \(\left( {MNP} \right)\parallel \left( {BCD} \right)\). Tính khoảng cách giữa hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {BCD} \right)\).
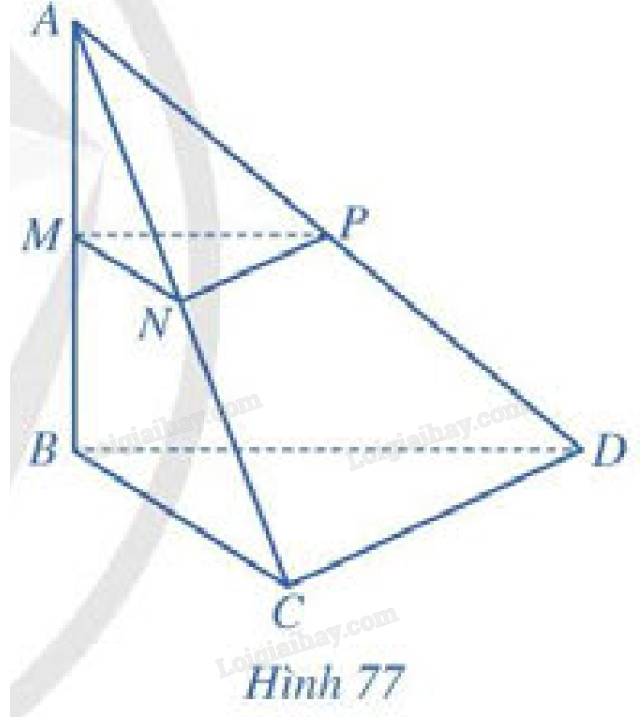
Cho hình tứ diện ABCD có AB a,BC b,BD c,widehat {ABC} widehat {ABD} widehat {BCD} {90^ circ }. Gọi M,N,P lần lượt là trung điểm của AB,AC,AD (Hình 77).a) Tính khoảng cách từ điểm C đến đường thẳng AB.b) Tính khoảng cách từ điểm D đến mặt phẳng left( {ABC} right).c) Tính khoảng cách giữa hai đường thẳng AB và C{rm{D}}.
Đọc tiếp
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).
a) Tính khoảng cách từ điểm \(C\) đến đường thẳng \(AB\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\).
c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(C{\rm{D}}\).