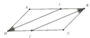
Cho hình bình hành ABCD (AB>DC), tia phân giác góc D cắt AB ở E, tia phân giác góc B cắt CD ở F
a. C/m: AE=CF
b. C/m: tứ giác DEBF là hình bình hành
c. C/M: AC,BD,EF đồng quy
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F. CMR:
a) DE // BF
b) Tứ giác DEBF là hình gì?
c) Tam giác ADE = Tam giác CBF
d) C/m: Tứ giác AECF là hình bình hành
e) AC, DB, EF đồng quy
a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)
\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)
mà \(\widehat{ADC}=\widehat{CBA}\)
nên \(\widehat{ADE}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=BC
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+DF=CD
mà AB=CD
và AE=CF
nên EB=DF
Xét tứ giác DEBF có
EB//DF
EB=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
d: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
e: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)
Ta có: EBFD là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy
cho hình bình hành ABCD, tia phân giác của góc D cắt Ab ở E .tia phân giác của góc B cắt Dc ở F
a/ chừng minh:DE//BF
b/chứng minh tứ giác DEBF là hình bình hành
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF và DE=BF
Ta có: AE+BE+AB
CF+FD=CD
mà AB=CD
và AE=CF
nên BE=FD
Xét tứ giác BEDF có
BE=DF
DE=BF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF
Bài 4. Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh DE // BF
b) Tứ giác DEBF là hình gì? Vì sao?
c) Chứng minh ba đường thẳng AC, BD, EF cùng đi qua 1 điểm.
Cho hình bình hành ABCD ( AB> BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a. c/m DE // BF
b. tứ giác DEBF là hình j
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng
a) AMCN là hình bình hành.
b) 3 đường AC, MN, BD đồng quy
a: Xét ΔDAM và ΔBCN có
\(\widehat{D}=\widehat{B}\)
DA=BC
\(\widehat{DAM}=\widehat{BCN}\)
Do đó: ΔDAM=ΔBCN
Suy ra: AM=CN và DM=BN
Ta có: AN+NB=AB
CM+MD=CD
mà AB=CD
và DM=BN
nên AN=CM
Xét tứ giác AMCN có
AN//CM
AM//CN
Do đó: AMCN là hình bình hành
Bài 1 : Cho hình bình hành ABCD ( AB > BC ) . Tia phân giác của góc D cắt AB ở E , tia phân giác của góc B cắt CD ở F . a ) Chứng minh DE // BF b ) Tứ giác DEBF là hình gì Bài 2 : Cho hình bình hành ABCD . gọi K , I lần lượt là trung điểm của các cạnh AB , CD . Gọi M , N lần lượt là giao điểm của AI , CK với đường chéo BD . Chứng minh AC , BD , IK đồng quy tại một điểm
Bài 2:
AK=AB/2
CI=CD/2
mà AB=CD
nên AK=CI
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,KI,BD đồng quy
Bài 1:
a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)
mà \(\widehat{ADC}=\widehat{ABC}\)
nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔEAD và ΔFCB có
\(\widehat{A}=\widehat{C}\)
AD=CB
\(\widehat{EDA}=\widehat{FBC}\)
Do đó: ΔEAD=ΔFCB
=>\(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{EDF}=\widehat{CFB}\)
mà hai góc này đồng vị
nên DE//BF
b: Xét tứ giác DEBF có
DE//BF
BE//DF
Do đó: DEBF là hình bình hành
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F. Tứ giác DEBF là hình gì? Vì sao?
Ta có: \(\widehat{ADE}=\widehat{CDE}=\dfrac{\widehat{ADC}}{2}\)(DE là phân giác của góc ADC)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{\widehat{ABC}}{2}\)(BF là phân giác của góc ABC)
mà \(\widehat{ADC}=\widehat{ABC}\)(ABCD là hình bình hành)
nên \(\widehat{ADE}=\widehat{CDE}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{EAD}=\widehat{FCB}\)(ABCD là hình bình hành)
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)(cmt)
Do đó: ΔADE=ΔCBF
=>AE=CF
Ta có: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên EB=FD
Ta có: AB//CD
E\(\in\)AB
F\(\in\)CD
Do đó: BE//DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M; tia phân giác của góc C cắt AB ở N
a, Chứng minh tứ giác AMCN là hình bình hành
b, Chứng minh 3 đường thẳng AC, MN, BD đồng quy
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh DE//BE.
b) Tứ giác DEBF là hình gì?
a) Ta có A E D ^ = E D C ^ v à A B F ^ = E D C ^ ⇒ D E / / B F (có góc ở vị trí đồng vị bằng nhau).
b) Từ câu a) suy ra DEBF là hình bình hành.