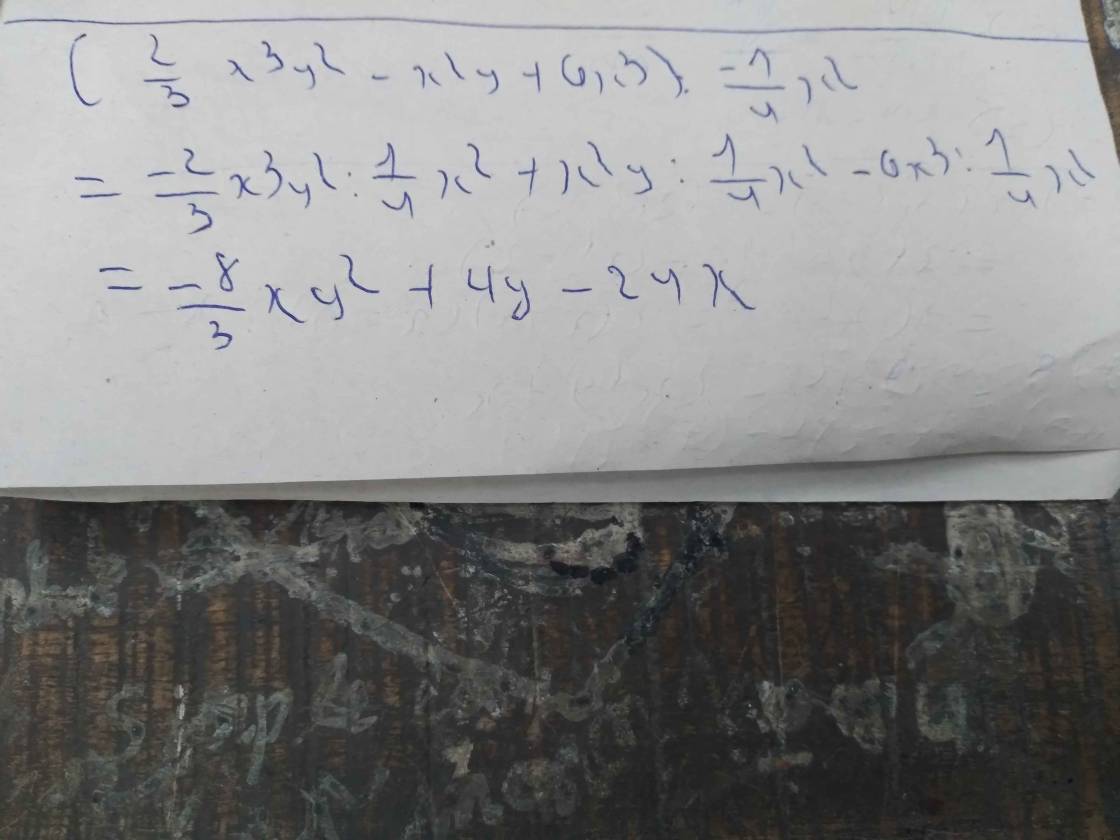Thực hiện phép tính: ( x-y )3 : ( y-x )2

Những câu hỏi liên quan
thực hiện phép tính sau\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 1
Bình luận (0)
1/x-y-3xy/x^3-y^3+x-y/x^2+xy+y^2
=1/x-y+-3xy/(x-y)(x^2+xy+y^2)+x-y/x^2+xy+y^2
=x^2+xy+y^2/(x-y)(x^2+xy+y^2)+-3xy/(x-y)(x^2+xy+y^2)+x^2-2xy+y^2/(x-y)(x^2+xy+y^2)
=x^2+xy+y^2-3xy+x^2-2xy-y^2/(x-y)(x^2+xy+y^2)
=2x^2-5xy/(x-y)(x^2+xy+y^2)
Đúng 0
Bình luận (0)
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 0
Bình luận (0)
1, Thực hiện phép tính
(\(\dfrac{2}{3}\)x\(^3\)y\(^2\)-x\(^2\)y+6x\(^3\)) : (\(\dfrac{-1}{4}\)x\(^2\))
thực hiện phép tính 2 x^ 2 y^ 2 .(- 4 x^ 5 y^3)kết quả là
Bài 1 Thực hiện phép tính rồi tính giá trị của biểu thức
a)A=x.(x+y)-x.(y-x) với x= -3 ; y=2
Ta có:
\(A=x\left(x+y\right)-x\left(y-x\right)=x^2+xy-xy+x^2=2x^2\)
Thay \(x=-3\) vào A, ta có:
\(A=2.\left(-3\right)^2=18\)
Vậy A=18
Đúng 2
Bình luận (0)
\(A=x\left(x+y\right)-x\left(y-x\right)=x\left(x+y\right)+x\left(x+y\right)=\left(x+y\right).2x=\left(-3+2\right).2.\left(-3\right)=6\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Thực hiện phép tính cộng
\(\dfrac{1}{x-y}\)+\(\dfrac{3xy}{y^3-x^3}\)+\(\dfrac{x-y}{x^2+xy+y^2}\)
GIÚP MÌNH VS Ạ
Ta có:
\(\dfrac{1}{x-y}+\dfrac{3xy}{y^3-x^3}+\dfrac{x-y}{x^2+xy+y^2}\\ =\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{x^3-y^3}\\ =\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\\ =\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 3
Bình luận (0)
\(\dfrac{1}{x-y}+\dfrac{3xy}{y^3-x^3}+\dfrac{x-y}{x^2+xy+y^2}\) \(=\dfrac{x^2+xy+y^2}{x^3-y^3}-\dfrac{3xy}{x^3-y^3}+\dfrac{\left(x-y\right)^2}{x^3-y^3}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{x^3-y^3}\)
\(=\dfrac{2x^2+2y^2-4xy}{x^3-y^3}\)
\(=\dfrac{2x^2-2xy-2xy+2y^2}{x^3-y^3}\)
\(=\dfrac{2x\left(x-y\right)-2y\left(x-y\right)}{x^3-y^3}\)
\(=\dfrac{\left(2x-2y\right)\left(x-y\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x-2y}{x^2+xy+y^2}\)
Đúng 1
Bình luận (0)
Thực hiện phép tính :bài 1 :thực hiện phép tính :
Bài 3: phân tích thành nhân tử:3/6x(x-y)-9y^2+9xyBài 4:Tìm x, biết:
1/ (x-1)(x^2+x+1)-x^3-6x=11
2/ 16x^2-(3x-4)^2=0
3/ x^3-x^2+3-3x=0
4/ x-1/x+2=x+2/x+1
5/1/x+2/x+1=0
6/ 9-x^2/x : (x-3)=1
Xem chi tiết
Bài 3: phân tích thành nhân tử:3/6x(x-y)-9y^2+9xyBài 4:Tìm x, biết:
1/ (x-1)(x^2+x+1)-x^3-6x=11
2/ 16x^2-(3x-4)^2=0
3/ x^3-x^2+3-3x=0
4/ x-1/x+2=x+2/x+1
5/1/x+2/x+1=0
6/ 9-x^2/x : (x-3)=1
Bài 3:
3: \(6x\left(x-y\right)-9y^2+9xy\)
\(=6x\left(x-y\right)+9xy-9y^2\)
\(=6x\left(x-y\right)+9y\left(x-y\right)\)
\(=\left(x-y\right)\left(6x+9y\right)\)
\(=3\left(2x+3y\right)\left(x-y\right)\)
Bài 4:



Đúng 1
Bình luận (0)
Thực hiện phép tính.
a) x^2 - 9 / 2x + 6 : 3-x / 2
b) 2x / x- y - 2y / x - y ( với y khác x)
\(a,=\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x+3\right)}\cdot\dfrac{2}{-\left(x-3\right)}=\dfrac{x-3}{2}\cdot\dfrac{2}{-\left(x-3\right)}=-1\\ b,=\dfrac{2x-2y}{x-y}=\dfrac{2\left(x-y\right)}{\left(x-y\right)}=2\)
Đúng 1
Bình luận (1)
a,\(\dfrac{x^2-9}{2x+6}:\dfrac{3-x}{2}=\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x+3\right)}.\dfrac{2}{3-x}=\dfrac{x-3}{3-x}=\dfrac{-\left(3-x\right)}{3-x}=-1\)
b, \(\dfrac{2x}{x-y}-\dfrac{2y}{x-y}=\dfrac{2x-2y}{x-y}=\dfrac{2\left(x-y\right)}{x-y}=2\)
Đúng 2
Bình luận (2)
Bài 3 ( 3đ) : Thực hiện phép tính
\(\dfrac{y}{x-y}-\dfrac{x^3-xy^2}{x^2+y^2}.\left(\dfrac{x}{x^2-2xy+y^2}-\dfrac{y}{x^2-y^2}\right)\)
Ta có: \(\dfrac{y}{x-y}-\dfrac{x^3-xy^2}{x^2+y^2}\cdot\left(\dfrac{x}{x^2-2xy+y^2}-\dfrac{y}{x^2-y^2}\right)\)
\(=\dfrac{y}{x-y}-\dfrac{x\left(x^2-y^2\right)}{x^2+y^2}\cdot\left(\dfrac{x\left(x+y\right)}{\left(x-y\right)^2\cdot\left(x+y\right)}-\dfrac{y\cdot\left(x-y\right)}{\left(x-y\right)^2\cdot\left(x+y\right)}\right)\)
\(=\dfrac{y}{x-y}-\dfrac{x\left(x-y\right)\left(x+y\right)}{x^2+y^2}\cdot\dfrac{x^2+xy-xy+y^2}{\left(x-y\right)^2\left(x+y\right)}\)
\(=\dfrac{y}{x-y}-\dfrac{x\cdot\left(x^2+y^2\right)}{\left(x^2+y^2\right)\cdot\left(x-y\right)}\)
\(=\dfrac{y}{x-y}-\dfrac{x}{x-y}\)
\(=\dfrac{y-x}{x-y}=\dfrac{-\left(x-y\right)}{x-y}=-1\)
Đúng 1
Bình luận (0)
Thực hiện các phép tính sau:
a) \(18{x^4}{y^3}:12{\left( { - x} \right)^3}y\)
b) \({x^2}{y^2} - 2x{y^3}:\left( {\dfrac{1}{2}x{y^2}} \right)\)
a) \(18x^4y^3:12\left(-x\right)^3y\)
\(=\left(18:-12\right)\left(x^4:x^3\right)\left(y^3:y\right)\)
\(=-\dfrac{3}{2}xy^2\)
b) \(x^2y^2-2xy^3:\dfrac{1}{2}xy^2\)
\(=\dfrac{xy^2\left(x-2y\right)}{\dfrac{1}{2}xy^2}\)
\(=\dfrac{x-2y}{\dfrac{1}{2}}\)
\(=2x-4y\)
Đúng 1
Bình luận (0)