Tìm phân số nghịch đảo của mỗi phân số sau:
a) \(\dfrac{-9}{19};\)
b) \(-\dfrac{21}{13};\)
c) \(\dfrac{1}{-9}.\)
Tìm số nghịch đảo của mỗi số hữu tỉ sau:
a)\(2\frac{1}{5}\); b)\( - 13\)
a)Ta có: \(2\frac{1}{5} = \frac{{11}}{5}\)
Số nghịch đảo của \(2\frac{1}{5}\) là: \(\frac{5}{{11}}\).
b) Số nghịch đảo của \( - 13\) là: \(\frac{{ - 1}}{{13}}\)
Chú ý: Ta phải chuyển hỗn số về phân số trước khi tìm số nghịch đảo.
Từ HĐ 2, em hãy tìm phân số nghịch đảo của 11 và \(\dfrac{7}{{ - 5}}\)
Phân số nghịch đảo của 11 là \(\dfrac{1}{{11}}\)
Phân số nghịch đảo của \(\dfrac{7}{{ - 5}}\) là \(\dfrac{{ - 5}}{7}\)
1)chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2
2)viết số nghịch đảo của -2 dưới dạng tổng các nghịch đảo của ba số nguyên khác nhau
3)cho hai phân số 8/15 và 18/35.Tìm số lớn nhất sao cho khi chia mỗi phân số này cho số đó ta được kết quả là số nguyên
4)tìm hai số biết rằng 9/11 của số này bằng 6/7 của số kia và tổng của hai số đó bằng 258
5)tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 6/7 và chia a cho 10/11 ta đều được kết quả là số tự nhiên
6)tìm hai số biết rằng 7/9 của số này bằng 28/33 của số kia và hiệu của hai số đó bằng 9
tìm số nghịch đảo của các số:1; -1; -5; 7; \(\dfrac{-3}{4}\);\(\dfrac{1}{-15}\);\(\dfrac{-2}{-7}\);\(-\dfrac{2}{19}\)
Số nghịch đảo của 1 là 1
Số nghịch đảo của -1 là -1
Số nghịch đảo của -5 là -1/5
Số nghịch đảo của 7 là 1/7
Số nghịch đảo của -3/4 là -4/3
Số nghịch đảo là 1/-15 là -15
Số nghịch đảo của -2/-7 là 7/2
Số nghịch đảo của -2/19 là -19/2
Bài 1: Nêu 2 cách viết phân số 14/19 thành tích của 5 phân số sao cho mỗi phân số đó có tử và mẫu là 2 số nguyên liên tiếp.
Bài 2: Cho tổng của 2 số bằng 2 và tích của chúng bằng 3. Hãy tìm tổng các nghịch đảo của 2 số đó.
Bài 3: Chứng minh rằng 3 < 1 + 1/2 + 1/3 + 1/4 +...+ 1/63 < 6.
Bài 4: Viết số nghịch đảo của 2 dưới dạng tổng các nghịch đảo của 3 số tự nhiên khác nhau.
Bài 5: Tìm phân số dương nhỏ nhất mà khi chia phân số này cho phân số ta được kết quả là 1 số tự nhiên.
MN GIÚP MIK IK! MAI MIK PHẢI NỘP RỒI!!!!!!!!!!!
Phân số nghịch đảo của 5/-9 là
Tìm phân thức nghịch đảo của mỗi phân thức sau:
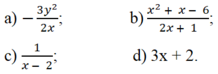
1.Cho các số 30,42,56,72,90,110.Tính tỏng các số nghịch đảo của các số trên một cách nhanh nhất.
2.Tìm phân số có giá trị nhỏ nhất đẻ khi nhân phân số này với mỗi phân số 2/3,4/5,6/7 thì mỗi tích tìm được đều là số tự nhiên
1) 1/30+1/42+1/56+1/72+1/90+1/110
=1/5*6+1/6*7+1/7*8+1/8*9+1/9*10+1/10*11
=1/5-1/6+1/6-1/7+...+1/10-1/11
=1/5-1/11=11/55-5/55=6/55
1 số nghịch đảo thì bit rồi nhé
Bây gời ta có:
1/30+1/42+1/56+1/72+1/90+1/110
=1/5.6+1/6.7+1/7.8+1/8.9+1/9.10+1/10.11
=1-1/5+1/5-1/6+1/6-1/7+1/7-1/8+1/8-1/9+1/9-1/10+1/10-1/11
=1-1/11
=10/11
Đó hiểu ko? ko hiểu chỗ nào thì hỏi mình nhé
a)Chứng minh rằng tổng của một phân số dương với nghịch đảo của nó không nhỏ hơn 2.
b) Tìm các phân số có tử và mẫu đều dương sao cho tổng của phân số đó với nghịch đảo của nó có giá trị nhỏ nhất.
a. Gọi phân số cần tìm là \(\frac{a}{b}\)
\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)
Theo bài ra, ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)
\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)
\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0
\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.