Trong bài học trên, đường đi của nhân vật là hinh tam giác đều. Đường đi đó có thể là hinh vuông, lục giác đều.... Khi đó các con số nào trong chương trình ở Hình 12.3 cầnphải thay đổi?
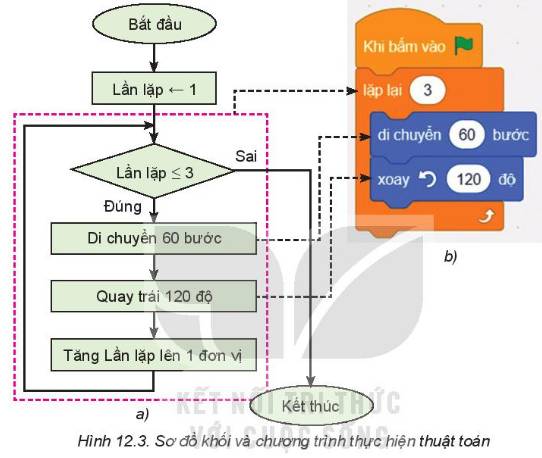
Trong Bài 12, em đã tạo ra chương trình để chú Bọ rùa đi chuyển theo đường đi là một tam gác đều. Làm thế nào để tổng quát bài toán với đường đi của nhân vật là một hình đa giác đều có số cạnh bắt kì được nhập vào từ bản phím?
Số cạnh của hình mà nhân vật di chuyển trong bài toán tổng quát ở là một biển, nó được đặt tên n và lưu trữ một giá trị số, chẳng hạn số 6.
Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC). Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC. Biết rằng khi điểm S thay đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C). Trong số các mặt cầu chứa đường tròn (C) , bán kính mặt cầu nhỏ nhất là
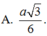
![]()
Người ta dựng một cái lều vải (H) có dạng hình chóp lục giác đều như hình vẽ bên. Đáy của (H) là một hình lục giác đều có độ dài cạnh là 3m.Chiều cao SO=6m (SO vuông góc với mặt đáy).Các cạnh bên của (H) là các sợi c 1 , c 2 , c 3 , c 4 , c 5 , c 6 nằm trên các parabol có trục đối xứng song song với SO.Giả sử giao tuyến (nếu có) của (H) với mặt phẳng (P) vuông góc với SO và một lục giác đều và khi (P) đi qua trung điểm của SO thì lục giác đều cạnh bằng 1.Tính thể tích không gian bên trong cái lều (H) đó.
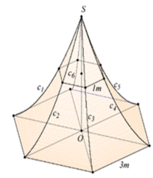
A. 135 3 5 m 3
B. 96 3 5 m 3
C. 135 3 4 m 3
D. 135 3 8 m 3
Trong mặt phẳng cho một hình lục giác đều cạnh bằng 2. Tính thể tích của hình tròn xoay có được khi quay hình lục giác đó quanh đường thẳng đi qua hai đỉnh đối diện của nó.
![]()
![]()
![]()
![]()
Bằng ngôn ngữ lập trình trực quan, bạn Khoa muốn tạo chương trình điều khiển nhân vật di chuyển theo đường đi là các hình như: tam giác đều, vuông,... Theo em, bạn Khoa cần thực hiện những công việc gì?
Theo em, bạn Khoa cần viết các bước cần thực hiện bằng ngôn ngữ tự nhiên. Sau đó, tạo chương trình máy tính thực hiện các bước đó
Cho đường tròn tâm (O), bán kính R ngoại tiếp đa giác dêdu của đường tròn A. Tính bán kính của đường tròn ngoại tiếp đa giác đó (A;R) trong trường hợp a, đa giác là tam giác đều b, đa giác là hình vuông c, đa giác là lục giác đều
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
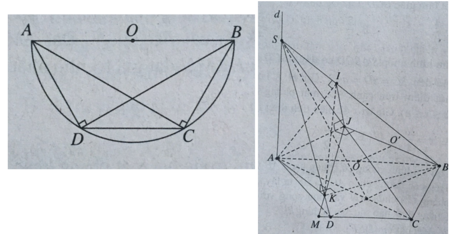
Nhận xét
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: ∠(ACB) = ∠(ADB) = 1v.
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)
Lý luận tương tự, ta có:
BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))
AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).
Cho hai tam giác cân chung đáy ABC và ABD, trong đó ABC là tam giác đều. Gọi E là trung điểm của AB. Khi đó, khẳng định nào sau đây là sai?
(A) Đường thẳng CD là đường trung trực của AB.
(B) Điểm E không nằm trên đường thẳng CD.
(C) Đường trung trực của AC đi qua B.
(D) Đường trung trực của BC đi qua A.
+) Do tam giác ABD cân tại D nên DA = DB ( định nghĩa tam giác cân).
Suy ra: D nằm trên đường trung trực của AB. (1)
+) Do tam giác ABC là tam giác đều nên CA = CB
Suy ra: C nằm trên đường trung trực của AB (2)
Từ (1) và (2)suy ra: CD là đường trung trực của AB.
+) Do E là trung điểm của AB nên EA = EB
Suy ra E nằm trên đường trung trực của AB
Suy ra, E nằm trên đường thẳng CD.
Do đó, (B) sai .
Chọn B.
Cho hình lục giác đều như hình 4.6.
Ta đã biết, 6 tam giác đều ghép lại thành hình lục giác đều, đó là những tam giác đều nào? Ngoài 6 tam giác đều đó, trong hình em còn thấy những tam giác đều nào khác?
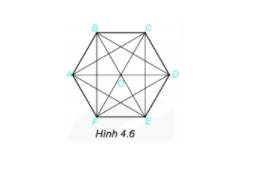
Các tam giác đều ghép thành hình lục giác đều là: tam giác ABO, tam giác BCO, tam giác CDO, tam giác DEO, tam giác EFO, tam giác FAO.
Trong hình còn có các tam giác đều: ACE, BDF.