cho hình vẽ biết góc E=110 độ góc B=70 góc C =40 độ. chứng minh DE//BC. tính góc EDC và góc xDC

Những câu hỏi liên quan
Cho hình vẽ, biết: E=110°. B=70° C = 40° a) Chứng minh: DE || BC; 110° b) Tính EDC và xDC.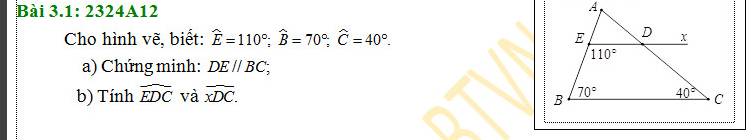
a) Ta thấy:
\(\widehat{BED}+\widehat{EBC}=180^o\)
Mà hai góc này ở vị trí trong cùng phía
\(\Rightarrow DE//BC\)
b) Mà: DE//BC
\(\Rightarrow\widehat{EDC}+\widehat{BCD}=180^o\)(hai góc trong cùng phía)
\(\Rightarrow\widehat{EDC}=180^o-\widehat{BCD}=180^o-40^o=140^o\)
Ta lại có:
\(\widehat{EDC}\) đối đỉnh \(\widehat{xDC}\)
\(\Rightarrow\widehat{xDC}=\widehat{EDC}=140^o\)
Đúng 2
Bình luận (2)
a) Ta có:
∠BED + ∠EBC = 110⁰ + 70⁰ = 180⁰
Mà ∠BED và ∠EBC là hai góc trong cùng phía
⇒ DE // BC
b) Do DE // BC
⇒ ∠EDC + ∠DCB = 180⁰ (hai góc trong cùng phía)
⇒ ∠EDC = 180⁰ - ∠DCB
= 180⁰ - 40⁰
= 140⁰
Do DE // BC
⇒ ∠xDC = ∠DCB = 40⁰ (so le trong)
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A = 40 độ. Trên tia đối cuả tia AC lấy điểm D . Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia Dx song song BC . Biết góc xDC = 70 độ
a>tính số đo góc ABC
b> vẽ tia Ay là tia phân giác góc BAD . Chứng minh góc Ay song song BC
Cho hình vuông ABCD, phía trong hình vuông, vẽ một tia Dx sao cho góc xDC15 độ. Gọi E là giao điểm của Dx và BC. M là trung ddieemer của DE.a) Chúng minh: Tam giác DMC cân và tính góc DMCb)Chúng minh: Tam giác MAB đềuCho hình vuông ABCD, phía trong hình vuông, vẽ một tia Dx sao cho góc xDC15 độ. Gọi E là giao điểm của Dx và BC. M là trung ddieemer của DE.a) Chúng minh: Tam giác DMC cân và tính góc DMCb)Chúng minh: Tam giác MAB đều
Đọc tiếp
Cho hình vuông ABCD, phía trong hình vuông, vẽ một tia Dx sao cho góc xDC=15 độ. Gọi E là giao điểm của Dx và BC. M là trung ddieemer của DE.
a) Chúng minh: Tam giác DMC cân và tính góc DMC
b)Chúng minh: Tam giác MAB đều
Cho hình vuông ABCD, phía trong hình vuông, vẽ một tia Dx sao cho góc xDC=15 độ. Gọi E là giao điểm của Dx và BC. M là trung ddieemer của DE.
a) Chúng minh: Tam giác DMC cân và tính góc DMC
b)Chúng minh: Tam giác MAB đều
Cho hình vẽ bên, biết góc NMP=110 độ, góc MPQ= 70 độ, góc MNQ= 125 độ
a) Chứng minh x//y
b) Tính số đo của góc Q1 ?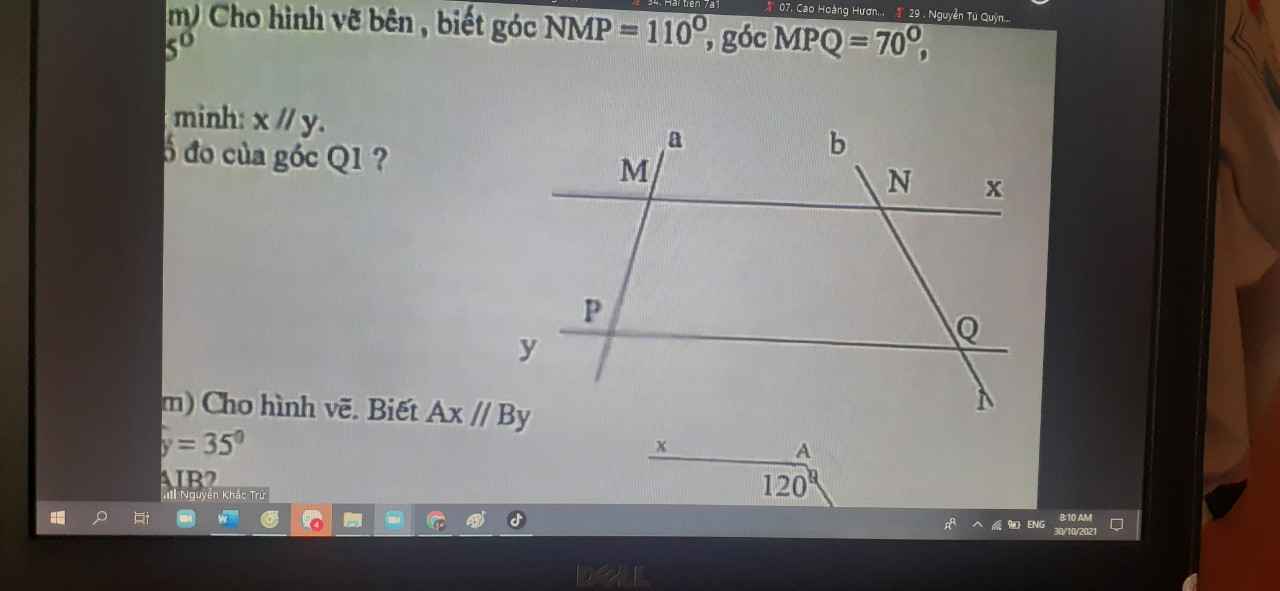
Cho tam giác ABC, góc C bằng 70 độ, góc A bằng 40 độ. Trên tia đối của tia AC lấy điểm O. Trên nửa mặt phẳng bờ AC có chứ B, vẽ tia Ox sao cho góc xOA bằng 110 độ.a, Chứng minh: Ox // BC.b, Kẻ At là tai p/giác của góc OAB. Chứng minh: At // BC.c, Kẻ tia AN là phân giác góc ABC. Chứng minh AN vuông góc với At.d, Chứng minh: AN vuông góc với BC, AN vuông góc với Ox.(Vẽ hình giúp mình nhé)
Đọc tiếp
Cho tam giác ABC, góc C bằng 70 độ, góc A bằng 40 độ. Trên tia đối của tia AC lấy điểm O. Trên nửa mặt phẳng bờ AC có chứ B, vẽ tia Ox sao cho góc xOA bằng 110 độ.
a, Chứng minh: Ox // BC.
b, Kẻ At là tai p/giác của góc OAB. Chứng minh: At // BC.
c, Kẻ tia AN là phân giác góc ABC. Chứng minh AN vuông góc với At.
d, Chứng minh: AN vuông góc với BC, AN vuông góc với Ox.
(Vẽ hình giúp mình nhé)
Cho ∆ABC nhọn đường cao AD. Vẽ DE vuông góc AB tại E, DF vuông góc AC tại F.
a) Chứng minh: AD2 = AB.AE và AB.AE = AC.AF
b) Chứng minh: ∆AEF đồng dạng ∆ACB.
c) Cho biết góc ABC 60 độ , góc ACB 45 độ , AD = 40 cm. Tính AB, AC, BC.
cho hình vẽ biết góc B = 40 độ, góc N = 110 độ, góc Q = 150 độ, góc R = 40 độ. a. Chứng tỏ MN song song với RQ. b. Tính góc NPQ?
1. Cho tam giác ABC có góc ABC 70 độ, góc ACB 40 độ.Vẽ tia Cx là tia đối của tia CB. Vẽ tia Cy là tia phân giác của góc Acx.1) Tính góc Acx, góc xAy.2) Chứng minh rằng: AB//Cy.2. Cho hình vẽ, biết góc BAC + góc ACD 180 độ ; góc BDC 70 độ.1) Chứng minh rằng: AB//CD.2) Tính góc ABD.3. Cho hình vẽ, biết góc BAD + góc ADC 180 độ ; góc ABC 90 độ.1) Chứng minh rằng: AB//CD2) Chứng minh rằng: BC vuông góc với CD.Giúp mình nhanh nhé!!!
Đọc tiếp
1. Cho tam giác ABC có góc ABC =70 độ, góc ACB =40 độ.Vẽ tia Cx là tia đối của tia CB. Vẽ tia Cy là tia phân giác của góc Acx.
1) Tính góc Acx, góc xAy.
2) Chứng minh rằng: AB//Cy.
2. Cho hình vẽ, biết góc BAC + góc ACD = 180 độ ; góc BDC = 70 độ.
1) Chứng minh rằng: AB//CD.
2) Tính góc ABD.
3. Cho hình vẽ, biết
góc BAD + góc ADC = 180 độ ; góc ABC = 90 độ.
1) Chứng minh rằng: AB//CD
2) Chứng minh rằng: BC vuông góc với CD.
Giúp mình nhanh nhé!!!
cho tam giác abc có góc a = 90 độ . tia phân giác bd của góc b ( d thuộc ac ) . trên bc lấy điểm e sao cho be = ba
a, so sánh ad và de
b, chứng minh góc edc = abc
c, chứng minh ae vuông góc với bd
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
Suy ra: DA=DE(hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)
hay DE⊥BC
Ta có: DA=DE(cmt)
mà DE<DC(ΔDEC vuông tại E có DC là cạnh huyền)
nên DA<DC
b) Ta có: ΔBAC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(1)
Ta có: ΔEDC vuông tại E(cmt)
nên \(\widehat{EDC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}=\widehat{EDC}\)(đpcm)
c) Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy ra BD là đường trung trực của AE
hay BD\(\perp\)AE(đpcm)
Đúng 1
Bình luận (0)















