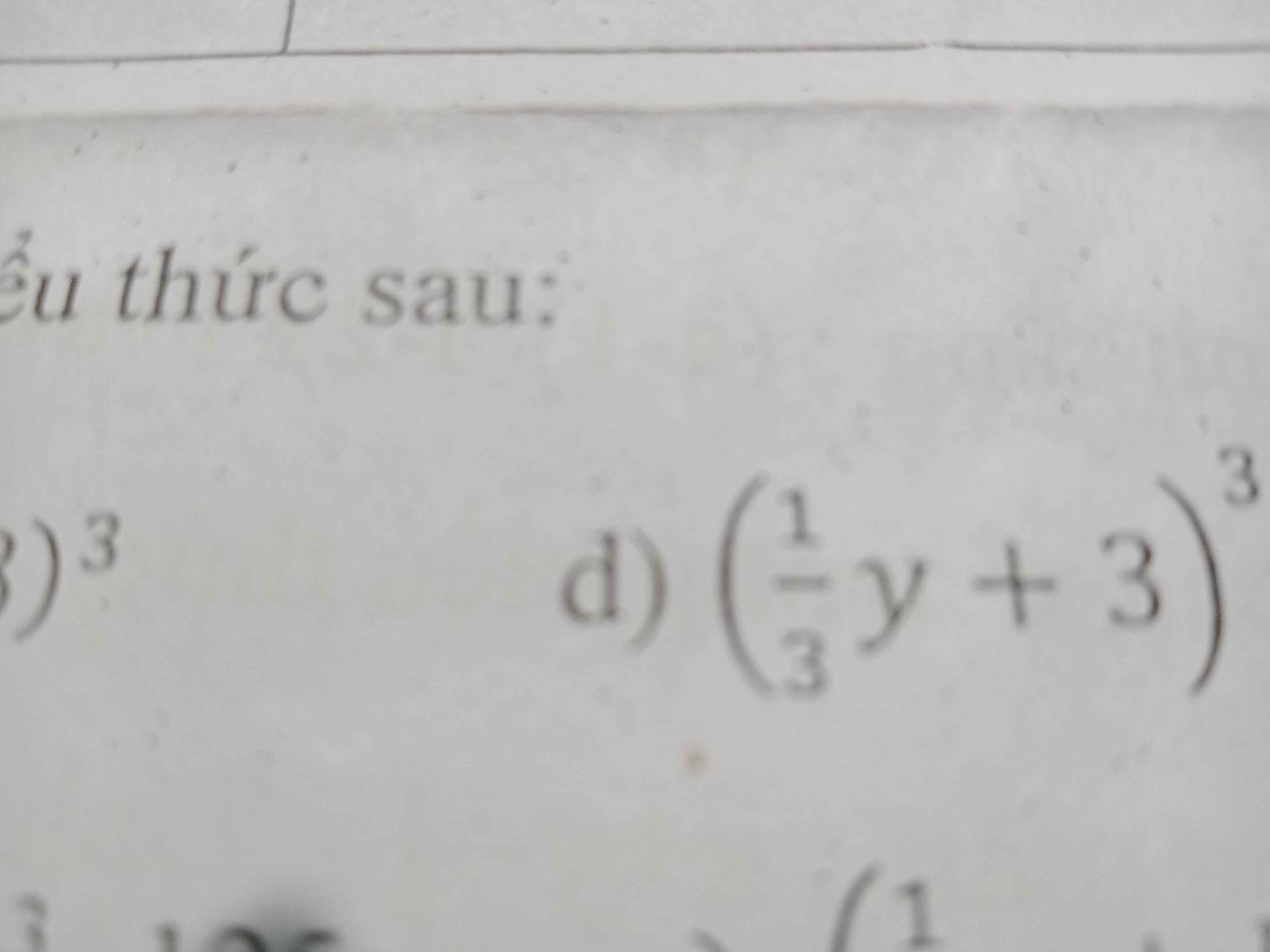
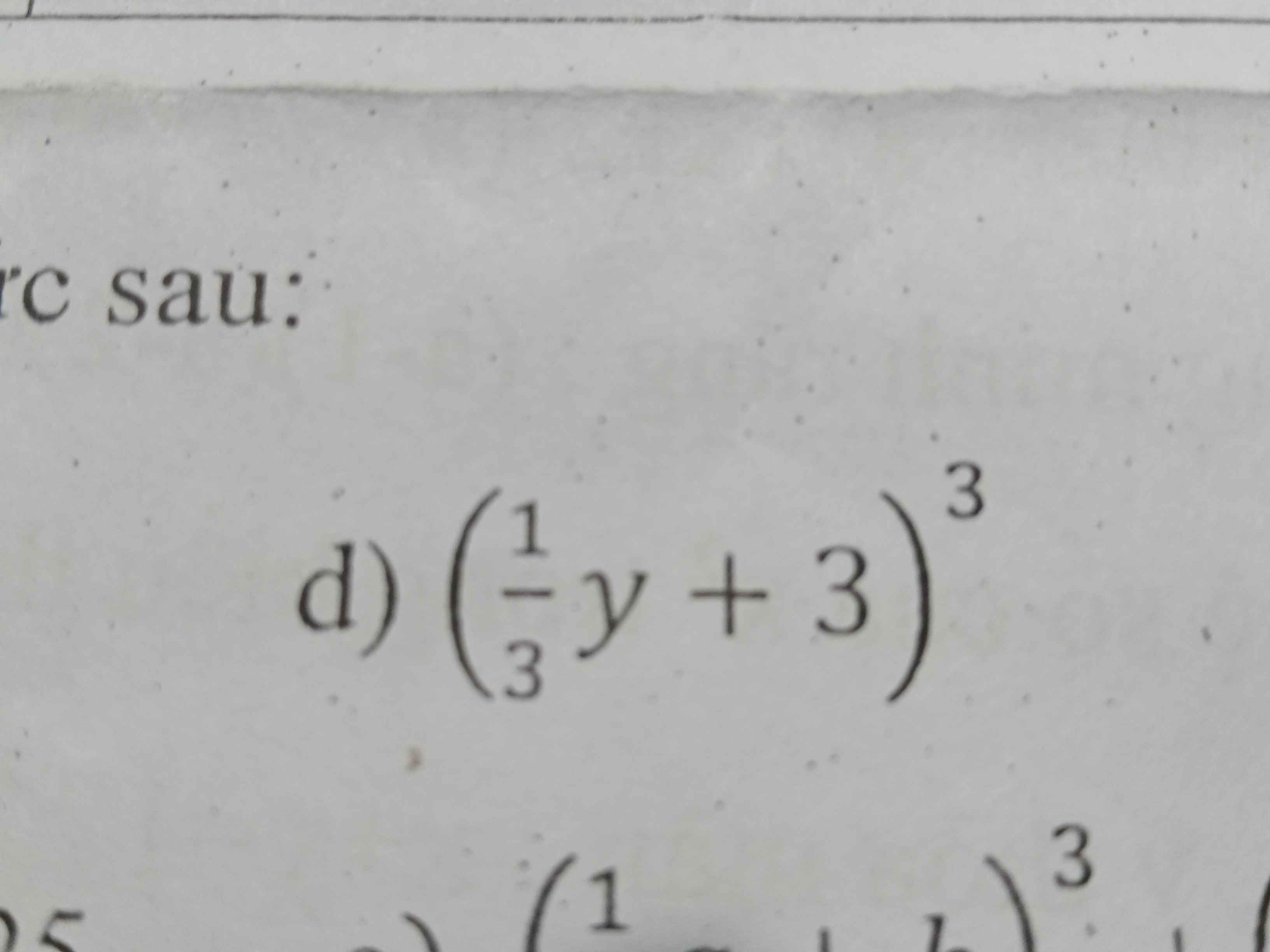
(1𝑦/3+3)^3

(𝑦/3+3)^3

(𝑦/3+3⋅3/3)^3

(𝑦+3⋅3/3)^3

(𝑦+9/3)^3

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

a) \(\left(3x^2-2y^3\right)^2\)

\(=\left(3x^2\right)^2-2\cdot3x^2\cdot2y^3+\left(2y^3\right)^2\)

\(=9x^4-12x^2y^3+4y^6\)

b) \(\left(-2x^2-3\right)^2\)

\(=\left(-2x^2\right)^2-2\cdot\left(-2x^2\right)\cdot3+3^2\)

\(=4x^4+12x^2+9\)

\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)

\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

a) \(\left(2x^2-1\right)^2=\left(2x^2\right)^2-2.2x^2.1+1^2\)

\(=4x^4-4x^2+1\).

b) \(\left(\frac{1}{2}x+3y^2\right)^2=\left(\frac{1}{2}x\right)^2+2.\frac{1}{2}x.3y^2+\left(3y^2\right)^2\)

\(=\frac{1}{4}x^2+3y^2x+9y^4\)

Chúc bn hc tốt!

a) \(12\left(2x-5\right)^2-3\left(1+4x\right)\left(4x-1\right)\)

\(=12\left[\left(2x\right)^2-2.2x.5+5^2\right]-3\left(4x+1\right)\left(4x-1\right)\)

\(=12\left(4x^2-20x+25\right)-3\left[\left(4x\right)^2-1\right]\)

\(=48x^2-240x+300-3\left(16x^2-1\right)\)

\(=48x^2-240x+300-48x^2+3\)

\(=-240x+303\)

A = (25+15).(25^2-15.25+15^2)/4 - 25.15

   = 40.475/4 - 375 = 10.475 - 375 = 4750 - 375 = 4375

k mk nha bạn ơi

a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)

\(=6x^2y+2y^3\)

\(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=\left(x+y-x+y\right)^3+3\left(x+y\right)\left(x-y\right)\left(x+y-x+y\right)\)

\(=8y^3+6y\left(x^2-y^2\right)\)

\(=8y^3+6x^2y-6y^3\)

\(=2y^3+6x^2y\)

a) $(3x+5)^2\\=(3x)^2+2.3x.5+5^2\\=9x^2+30x+25$

b) $(6x+\dfrac{1}{3})^2\\=(6x)^2+2.6x.\dfrac{1}{3}+(\dfrac{1}{3})^2\\=36x^2+4x+\dfrac{1}{9}$

c) $(5x-4y)^2\\=(5x)^2-2.5x.4y+(4y)^2\\=25x^2-40xy+16y^2$

d) $(5x-3)(5x+3)\\=(5x)^2-(3)^2\\=25x^2-9$