Phân tích đa thức \({x^3} - x\) thành nhân tử.
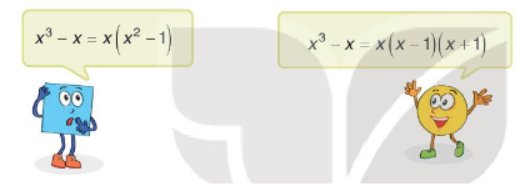
Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.
Khi thảo luận nhóm, một bạn ra đề bài: Hãy phân tích đa thức x4 - 9x3 + x2 - 9x thành nhân tử
Bạn Thái làm như sau:
x4 - 9x3 + x2 – 9x = x(x3 - 9x2 + x – 9).
Bạn Hà làm như sau:
x4 - 9x3 + x2 – 9x = (x4 - 9x3) + (x2 – 9x)
= x3(x – 9) + x(x – 9) = (x – 9)(x3 + x).
Bạn An làm như sau:
x4 - 9x3 + x2 – 9x = (x4 + x2) - (9x3 + 9x) = x2(x2 + 1) – 9x(x2 + 1)
= (x2 – 9x) (x2 + 1)= x(x – 9)(x2 + 1).
Hãy nêu ý kiến của em về lời giải của các bạn
Lời giải của các bạn đều thỏa mãn yêu cầu đề bài là phân tích đa thức thành nhân tử
Tìm x ( áp dùng kiến thức phân tích đa thức thành nhân tử )
a, x^3+3x^2+3x=0
bx^3+6x62+12x=0
mn giúp em với:(
a) \(x^3+3x^2+3x=0\Rightarrow x\left(x^2+3x+3\right)=0\Rightarrow x\left[\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\Rightarrow x=0\)
(do \(\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\))
b) \(x^3+6x^2+12x=0\Rightarrow x\left(x^2+6x+12\right)=0\Rightarrow x\left[\left(x+3\right)^2+4\right]=0\Rightarrow x=0\)
(do (x+3)2+4≥4>0)
a: Ta có: \(x^3+3x^2+3x=0\)
\(\Leftrightarrow x\left(x^2+3x+3\right)=0\)
hay x=0
b: Ta có: \(x^3+6x^2+12x=0\)
\(\Leftrightarrow x\left(x^2+6x+12\right)=0\)
hay x=0
tìm x biết:
(x^2+2x)^2-2x^2-4x-3=0
bài này áp dụng kiến thức phân tích đa thức thành nhân tử, mn giúp em với
\(\left(x^2+2x\right)^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+4x^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+2x^2-4x-3=0\Leftrightarrow\left(x-1\right)\left(x+1\right)^2\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)
Ta có: \(\left(x^2+2x\right)^2-2x^2-4x-3=0\)
\(\Leftrightarrow\left(x^2+2x\right)^2-2\left(x^2+2x\right)-3=0\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-3\\x=1\end{matrix}\right.\)
\(x^3+y^3+6x^2+12x+8\)
em hãy phân tích đa thức trên thành nhân tử
\(=\left(x+2\right)^3+y^3\)
\(=\left(x+2+y\right)\left(x^2+4x+4-xy-2y+y^2\right)\)
\(x^3+y^3+6x^2+12x+8\)
=\(x^3+3.2.x^2+3.2^2.x+2^3+y^3\)
\(=\left(x+2\right)^3+y^3=\left(x+2+y\right)\left(\left(x+2\right)^2-\left(x+2\right)y+y^2\right)\)
\(=\left(x+y+2\right)\left(x^2+4x+4-xy-2y-y^2\right)\)
2 câu này khó quá mn giúp em với ạ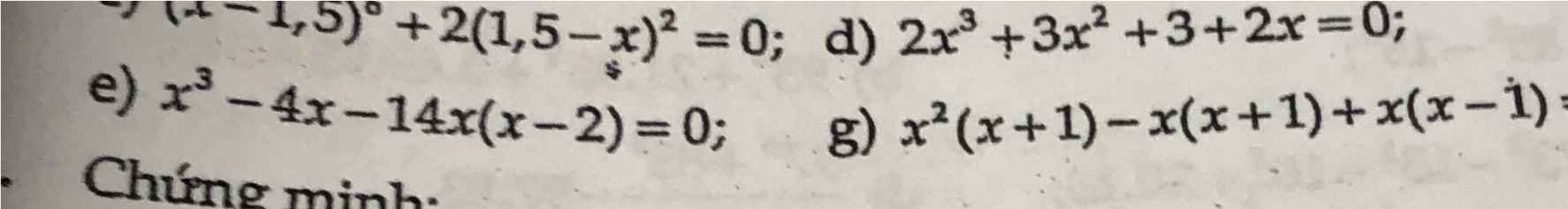
cái cuối của câu g còn có - 0 nữa nha mn
Đề bài là tìm x, áp dụng kiến thức phân tích đa thức thành nhân tử
e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)
Phân tích đa thức thành nhân tử:
\(x\)2\(+x-6\)
Giải chi tiết giúp em. Cảm ơn ạ
Tham khảo:https://hoc247.net/hoi-dap/toan-8/phan-tich-da-thuc-x-7-x-2-1-thanh-nhan-tu-faq417522.html
\(=x^7+x^6-x^6+x^5-x^5+x^4-x^4+x^3-x^3+x^2+x^2-x^2+x-x+1\\ =\left(x^7+x^6+x^5\right)-\left(x^6+x^5+x^4\right)+\left(x^4+x^3+x^2\right)-\left(x^3+x^2+x\right)+\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)
Lời giải:
$x^2+x-6=(x^2-2x)+(3x-6)=x(x-2)+3(x-2)=(x-2)(x+3)$
tìm x biết a, x^4 - 16x^2 = 0 b,x^8 +36x^4 = 0 c,,(x-5)^3-x+5 = 0 d, 5(x-2) -x^2 +4=0 Đây là kiến thức phân tích đa thức thành nhân tử, mn giúp em với
a) Ta có: \(x^4-16x^2=0\)
\(\Leftrightarrow x^2\left(x^2-16\right)=0\)
\(\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
b) Ta có: \(x^8+36x^4=0\)
\(\Leftrightarrow x^4\left(x^4+36\right)=0\)
\(\Leftrightarrow x^4=0\)
hay x=0
c) Ta có: \(\left(x-5\right)^3-x+5=0\)
\(\Leftrightarrow\left(x-5\right)\cdot\left[\left(x-5\right)^2-1\right]=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\\x=6\end{matrix}\right.\)
d) Ta có: \(5\left(x-2\right)-x^2+4=0\)
\(\Leftrightarrow5\left(x-2\right)-\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(5-x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Phân tích đa thức sau thành nhân tử ( mn giải từng bước ra giùm em vs ạ ): 2x(x- y) - 10y(x - y)
2x ( x - y ) - 10y ( x - y )
= ( x - y ) ( 2x - 10y )
= ( x - y ) ( 2 . x - 2 . 5y )
= ( x - y ) ( x - 5y ) 2
2x ( x - y ) - 10y ( x - y )
= ( x - y ) ( 2x - 10y )
= ( x - y ) ( 2 . x - 2 . 5y )
= ( x - y ) ( x - 5y ) 2
Phân tích đa thức thành nhân tử:
1)x^3-2x^2+2x-13
2)x^2-2xy+y^2-xy+yz
3)x^3-x^2-5x+12
Xin hãy giúp mình!!!
1, \(^{x^3-2x^2+2x-13
}\)
\(=x.\left(x^2-2x+2\right)-13\)
\(=x.\left(x^2+2\right)-13\)
3,\(x^3-x^2-5x+12\)
\(=x.\left(x^2-x-5\right)+12\)
\(=x.\left(x-5\right)+12\)
mình chỉ giúp bạn được như vậy thôi mong bạn thông cảm chúc bạn học tốt
bài này áp dụng kiến thức phân tích đa thức thành nhân tử, em thấy khá rối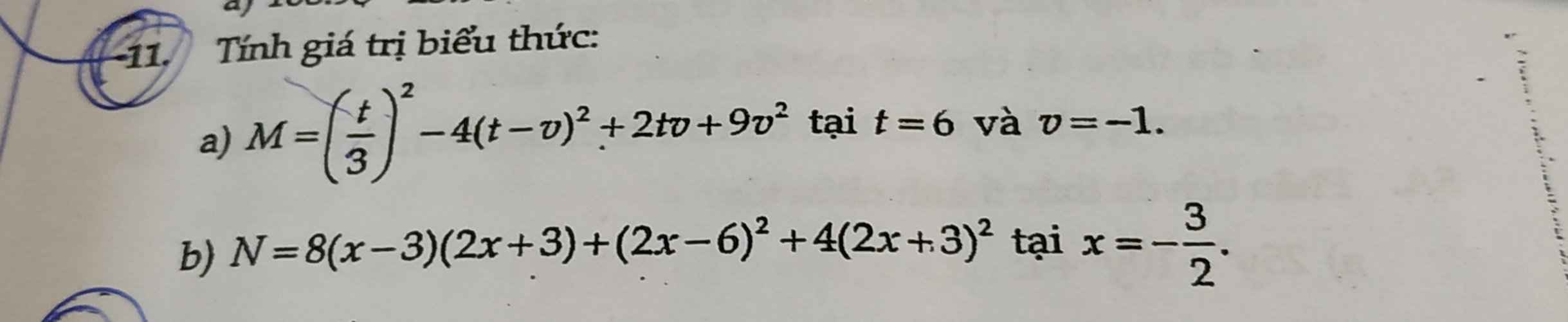
\(M=\left(\dfrac{1}{3}t\right)^2-4\left(t-v\right)^2+2tv+9v^2\)
\(=\left(\dfrac{1}{3}\cdot6\right)^2-4\cdot\left(6+1\right)^2+2\cdot6\cdot\left(-1\right)+9\)
\(=4-28-12+9\)
=-27
\(N=8\left(x-3\right)\left(2x+3\right)+\left(2x-6\right)^2+4\left(2x+3\right)^2\)
\(=8\left(2x^2+3x-6x-9\right)+4x^2-24x+36+4\left(4x^2+12x+9\right)\)
\(=8\left(2x^2-3x-9\right)+4x^2-24x+36+16x^2+48x+36\)
\(=16x^2-24x-9+20x^2+24x+72\)
\(=36x^2\)
\(=36\cdot\dfrac{9}{4}=81\)
a. \(M=\left(\dfrac{t}{3}\right)^2+2tv+9v^2-4\left(t-v\right)^2\)
\(=\left(\dfrac{t}{3}+3v\right)^2-4\left(t-v\right)^2\)
\(=\left(\dfrac{t}{3}+3v-2t+2v\right)\left(\dfrac{t}{3}+3v+2t-2v\right)\)
\(=\left(\dfrac{t}{3}+5v-2t\right)\left(\dfrac{t}{3}+v+2t\right)\)
Thay \(t=6\) và \(v=-1\) vào \(M\), ta được
\(M=\left(2-5-12\right)\left(2-1+12\right)=-15.13=-195\)
b. \(N=8\left(x-3\right)\left(2x+3\right)+\left(2x-6\right)^2+4\left(2x+3\right)^2\)
\(=\left(2x-6\right)^2+2.\left(2x-6\right)2\left(2x+3\right)+4\left(2x+3\right)^2\)
\(=\left(2x-6+4x+6\right)^2=\left(6x\right)^2=36x^2\)
Thay \(x=-\dfrac{3}{2}\) vào \(M\), ta được
\(M=36.\left(-\dfrac{3}{2}\right)^2=\dfrac{36.9}{4}=81\)