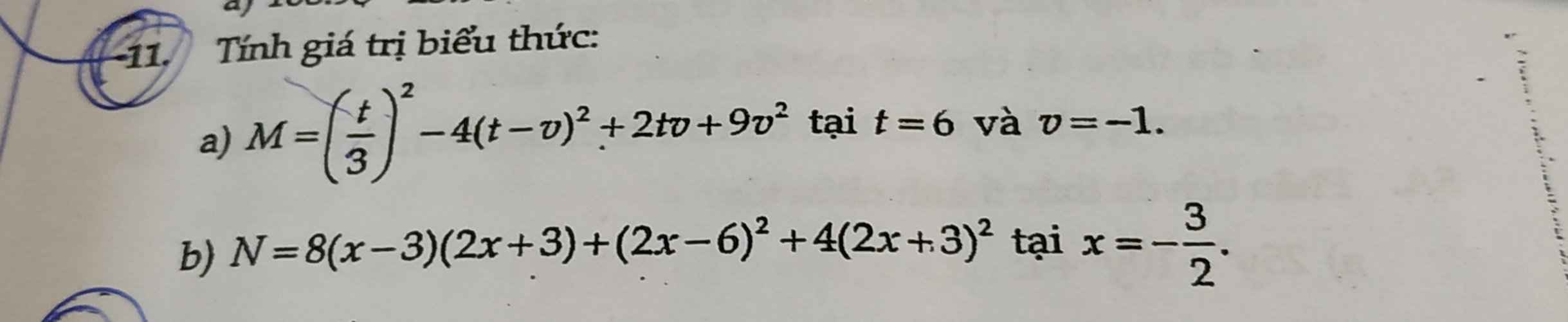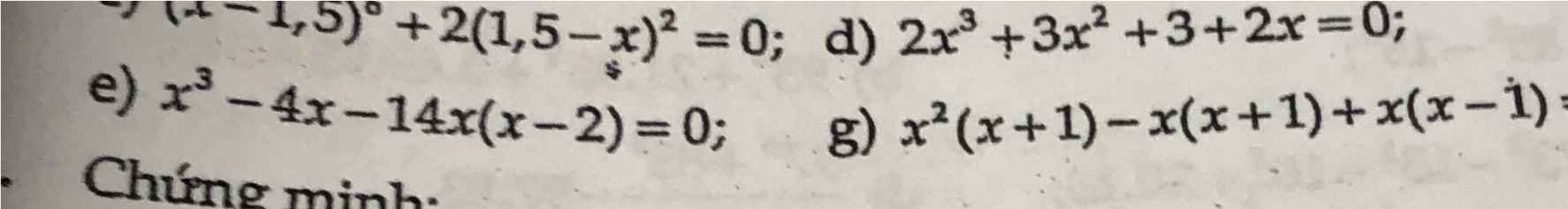\(M=\left(\dfrac{1}{3}t\right)^2-4\left(t-v\right)^2+2tv+9v^2\)
\(=\left(\dfrac{1}{3}\cdot6\right)^2-4\cdot\left(6+1\right)^2+2\cdot6\cdot\left(-1\right)+9\)
\(=4-28-12+9\)
=-27
\(N=8\left(x-3\right)\left(2x+3\right)+\left(2x-6\right)^2+4\left(2x+3\right)^2\)
\(=8\left(2x^2+3x-6x-9\right)+4x^2-24x+36+4\left(4x^2+12x+9\right)\)
\(=8\left(2x^2-3x-9\right)+4x^2-24x+36+16x^2+48x+36\)
\(=16x^2-24x-9+20x^2+24x+72\)
\(=36x^2\)
\(=36\cdot\dfrac{9}{4}=81\)
a. \(M=\left(\dfrac{t}{3}\right)^2+2tv+9v^2-4\left(t-v\right)^2\)
\(=\left(\dfrac{t}{3}+3v\right)^2-4\left(t-v\right)^2\)
\(=\left(\dfrac{t}{3}+3v-2t+2v\right)\left(\dfrac{t}{3}+3v+2t-2v\right)\)
\(=\left(\dfrac{t}{3}+5v-2t\right)\left(\dfrac{t}{3}+v+2t\right)\)
Thay \(t=6\) và \(v=-1\) vào \(M\), ta được
\(M=\left(2-5-12\right)\left(2-1+12\right)=-15.13=-195\)
b. \(N=8\left(x-3\right)\left(2x+3\right)+\left(2x-6\right)^2+4\left(2x+3\right)^2\)
\(=\left(2x-6\right)^2+2.\left(2x-6\right)2\left(2x+3\right)+4\left(2x+3\right)^2\)
\(=\left(2x-6+4x+6\right)^2=\left(6x\right)^2=36x^2\)
Thay \(x=-\dfrac{3}{2}\) vào \(M\), ta được
\(M=36.\left(-\dfrac{3}{2}\right)^2=\dfrac{36.9}{4}=81\)