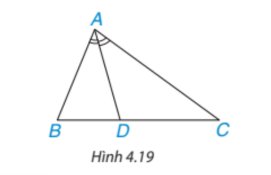
Trong H.4.19, AD là đường phân giác của tam giác ABC. Hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\) có bằng nhau không?
Những câu hỏi liên quan
23 tháng 1 2022 lúc 9:45
Cho tam giác ABC có các đường phân giác AD,BE,CF(D ∈ BC, E ϵ AC, F ∈ AB). Tính \(\dfrac{DB}{DC}.\dfrac{EC}{EA}.\dfrac{FA}{FB}=?\)
áp dụng định lý phân giác ta có:\(\left\{{}\begin{matrix}\dfrac{DB}{DC}=\dfrac{AB}{AC}\\\dfrac{EC}{EA}=\dfrac{BC}{AB}\\\dfrac{FA}{FB}=\dfrac{AC}{BC}\end{matrix}\right.\)
\(\dfrac{DB}{DC}.\dfrac{EC}{EA}.\dfrac{FA}{FB}=\dfrac{AB}{AC}.\dfrac{BC}{AB}.\dfrac{AC}{BC}=1\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có AB =6 cm ,AC = 9cm ,BC = 10 cm ,đường phân giác trong AD , đường phân giác ngoài AE.
a ) Tính DB, DC , EB
b ) Đường phân giác CF của tam giác ABC cắt AD ở I .Tính tỉ số diện tích tam giác DIF và diện tích tam giác ABC
Help mình với
#Toán lớp 8
a, Vì AD là phân giác nên \(\frac{AB}{AC}=\frac{DB}{DC}\Rightarrow\frac{DC}{AC}=\frac{DB}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\frac{DC}{AC}=\frac{DB}{AB}=\frac{BC}{AB+AC}=\frac{10}{15}=\frac{2}{3}\Rightarrow DC=6cm;DB=4cm\)
cho ΔABC có đg phân giác AD, ta có tỉ số:
A. \(\dfrac{AB}{BD}=\dfrac{DC}{AC}\) B.\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) C.\(\dfrac{DC}{BD}=\dfrac{AB}{AC}\) D.\(\dfrac{AB}{DB}=\dfrac{AC}{DC}\)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có AB 6cm, AC 8cm, AD là tia phân giác của góc BAC (D ϵ BC)a, Tính tỉ số dfrac{DB}{DC} và độ dài các đoạn thẳng BC, DB, DCb, TỪ D kẻ DE vuông góc với AB tại E (E ϵ AB). Tính độ dài AE, DE và diện tích tứ giác AEDCc, Gọi O là giao điểm của AD và CE. QUa O kẻ đường thằng song song với AC cắt BC và AB lần lượt tại M và N. Chứng minh rằng OM ON
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm, AD là tia phân giác của góc BAC (D ϵ BC)
a, Tính tỉ số \(\dfrac{DB}{DC}\) và độ dài các đoạn thẳng BC, DB, DC
b, TỪ D kẻ DE vuông góc với AB tại E (E ϵ AB). Tính độ dài AE, DE và diện tích tứ giác AEDC
c, Gọi O là giao điểm của AD và CE. QUa O kẻ đường thằng song song với AC cắt BC và AB lần lượt tại M và N. Chứng minh rằng OM = ON
a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DB}{DC}=\dfrac{6}{8}=\dfrac{3}{4}\)
Đúng 0
Bình luận (0)
17 tháng 7 2021 lúc 8:38
Cho tam giác ABC (AB<AC) có đường cao AH và đường phân giác AD. Trên cạnh AC, lấy 1 điểm E sao cho AE=AB. Nối BE cắt AH tại I.
a) Chứng minh \(\dfrac{HB}{HC}=\dfrac{IB^2}{IE^2}\)
b) Cho DB= 15cm, DC=20cm. Tính chu vi và diện tích của tứ giác AEDI
Cho tam giác ABC có M là đường trung tuyến của tam giác AMB cắt AB tại D tia phân giác của A = C cắt AC tạI E . Biết AM = 4cm , BC =12cm
a, tính \(\dfrac{AD}{DB}\)
b, so sánh \(\dfrac{AD}{DB}\)và \(\dfrac{AE}{EC}\)
c, chứng minh DE// BC
a: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{BM}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\left(1\right)\)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Ta có: M là trung điểm của BC
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
c: Xét ΔABC có
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB =6 cm ,AC = 9cm ,BC = 10 cm ,đường phân giác trong AD , đường phân giác ngoài AE.
a ) Tính DB, DC , EB
b ) Đường phân giác CF của tam giác ABC cắt AD ở I .Tính tỉ số diện tích tam giác DIF và diện tích tam giác ABC
30 tháng 3 2022 lúc 8:17
Cho tam giác ABC, đường phân giác AD. Biết AB = 16 cm, AC = 12 cm.
a. Tính tỉ số DB và DC.
b. Từ D kẻ đường thẳng song song với AC cắt AB tại H. Biết DB = 4 cm, DC = 3 cm. Tính DH ?
a. -△ABC có AD là phân giác \(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{16}{12}=\dfrac{4}{3}\)
b. -△ABC có DH//AC \(\Rightarrow\dfrac{DH}{AC}=\dfrac{BD}{BC}=\dfrac{BD}{BD+CD}\)
\(\Rightarrow\dfrac{DH}{12}=\dfrac{4}{4+3}\Rightarrow DH=\dfrac{12.4}{4+3}=\dfrac{48}{7}\left(cm\right)\)
Đúng 3
Bình luận (0)
cho tam giác ABC, AC=9cm,BC=10cm,AB=6cm, đường phân giác trong AD, đường phân giác ngoài AE
a) tính DB,DC,BE
b)đường phân giác CF của tg ABC cắt AD ở I. tính tỉ số diện tích tg DIF và ABC