Parabol và đường thẳng có một điểm chung duy nhất thì hoành độ của điểm đó là:

Những câu hỏi liên quan
cho parabol(P) y=1/2x2 và đường thẳng (d) có phương trình y=2x-2 chứng tỏ rằng đường thẳng (d) parabol (P) có điểm chung duy nhất xác định tọa độ điểm chung đó
Trong mặt phẳng toạ độ cho parabol y=x^2 và đường thẳng y=2mx-m^2+m-1
.
a. Tìm toạ độ giao điểm của (P) và (d) khi .
b. Tìm để (P) cắt (d) tại hai điểm phân biệt.
c. Tìm để (P) và (d) có một điểm chung duy nhất.
d. Tìm để (P) cắt (d) tại điểm có hoành độ bằng 2.
Cho đường thẳng d có phương trình y = ax + b biết rằng đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 1 và song song với đường thẳng y = -2x + 2003
1. Tìm a và b
2. Tìm tọa độ các điểm chung nếu có của d và parabol p: y=-1/2x^2
a) Vì (d) song song với đường thẳng \(y=-2x+2003\Rightarrow\left\{{}\begin{matrix}a=-2\\b\ne2003\end{matrix}\right.\)
\(\Rightarrow\left(d\right):y=-2x+b\)
Vì (d) cắt trục hoành tại điểm có hoành độ = 1
\(\Rightarrow\) tọa độ điểm đó là \(\left(1;0\right)\)
\(\Rightarrow1=b\Rightarrow\left(d\right):y=-2x+1\)
b) pt hoành độ giao điểm: \(-\dfrac{1}{2}x^2=-2x+2\Rightarrow\dfrac{1}{2}x^2-2x+2=0\)
\(\Rightarrow x^2-4x+4=0\Rightarrow\left(x-2\right)^2=0\Rightarrow x=2\Rightarrow y=-\dfrac{1}{2}.2^2=-2\)
\(\Rightarrow\) tọa độ giao điểm là \(\left(2;-2\right)\)
Đúng 1
Bình luận (0)
cho (P) y=mx^2 và đường thẳng (d) có hệ số góc là 2 .biết (d) và (P) có 1 điểm chung duy nhất là A có hoành độ là 2 vậy tung độ điểm A là bao nhiêu
a) Xác định các hệ số a, b của hàm số y=ax+b biết rằng đồ thị của nó đi qua điểm A(2;1) và cắt trục tung tại điểm có tung độ bằng 5.
b) Cho parabol (P): y= 3x^2 và đường thẳng (d): y=2x+m ( m là tham số ). Tìm m để (P) và (d) có 1 điểm chung duy nhất. Tìm tọa độ điểm chung đó.
a) Ta có: đồ thị hàm số y=ax+b đi qua điểm A (2:1)
=> 2a+b=1 (1)
Lại có: đồ thị cắt trục tung tại điểm có tung độ bằng 5
=> b=5 (2)
Từ (1) và (2) ta có: 2a+5=1
=> a= -2
b) Gía trị của m để (P) và (d) có 1 điểm chung duy nhất là
3x2 =2x+m
=> 3x2-2x-m
\(\Delta'=1+3m\)
=> m= -1/3
Tọa độ điểm chung là:
3x2=2x-1/3
=> 3x2-2x+1/3
=> x=1/3
thay x=1/3 vào vào parabol (P) ta đc: y= 3(1/3)2
y=1/3
=> Tọa độ ddiemr chung là (1/3; 1/3)
Cho parabol \(P ( P ) : y = x ^2\) và đường thẳng (d)\(: y = k x − k + 1 \) Tìm các giá trị của k để (P) và (d) luôn cắt nhau tại hai điểm phan biệt, trong đó có ít nhất một điểm có hoành độ dương .
Phương trình hoành độ giao điểm:
\(x^2=kx-k+1\Leftrightarrow x^2-kx+k-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-k\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1-k\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=k-1\end{matrix}\right.\)
\(\Rightarrow\) (P) cắt (d) tại 2 điểm pb khi \(k-1\ne1\Rightarrow k\ne2\), khi đó ta luôn có ít nhất 1 điểm có hoành độ dương là x=1
Đúng 0
Bình luận (0)
Cho parabol (P):
y
1
−
2
m
2
x
2
và đường thẳng (d): y 2x + 2. Biết đường thẳng d cắt (P) tại một điểm có tung độ y 4. Tìm hoành độ giao điểm còn lại của d và parabol (P) A.
x
−
1
2
B.
x
1...
Đọc tiếp
Cho parabol (P): y = 1 − 2 m 2 x 2 và đường thẳng (d): y = 2x + 2. Biết đường thẳng d cắt (P) tại một điểm có tung độ y = 4. Tìm hoành độ giao điểm còn lại của d và parabol (P)
A. x = − 1 2
B. x = 1 2
C. x = − 1 4
D. x = 1 4
Thay y = 4 vào phương trình đường thẳng d ta được 2x + 2 = 4 ⇔ x = 1
Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (1; 4)
Thay x = 1; y = 4 vào hàm số y = 1 − 2 m 2 x 2 ta được:
1 − 2 m 2 .1 2 = 4 ⇔ 1 – 2m = 8 ⇔ m = − 7 2
Xét phương trình hoành độ giao điểm của d và (P):
4x2 = 2x + 2 ⇔ 2x2 – x – 1 = 0
⇔ (2x + 1) (x – 1) = 0
⇔ x = 1 x = − 1 2
Vậy hoành độ giao điểm còn lại là
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho parabol
(
P
)
:
y
1
2
x
2
và đường tròn (C) có bán kính bằng 1 tiếp xúc với trục hoành đồng thời có chung một điểm A duy nhất với (P). Diện tích hình phẳng giới hạn bởi (P), (C) và trục hoành(phần bôi đậm trong hình vẽ) bằng A.
3
3
+
2...
Đọc tiếp
Cho parabol ( P ) : y = 1 2 x 2 và đường tròn (C) có bán kính bằng 1 tiếp xúc với trục hoành đồng thời có chung một điểm A duy nhất với (P). Diện tích hình phẳng giới hạn bởi (P), (C) và trục hoành(phần bôi đậm trong hình vẽ) bằng
A. 3 3 + 2 - π 3
B. 29 3 - 9 π 24
C. 9 3 + 9 - 4 π 12
D. 27 3 - 8 π 24
Ta cần tìm phương trình của đường tròn:
Vì đường tròn có bán kính bằng 1 và tiếp xúc với trục hoành nên tâm của đường tròn là I(t;1), (t > 0) phương trình của đường tròn là x - 1 2 + y - 1 2 = 1 .
Theo giả thiết đường tròn (C) có chung một điểm AA duy nhất với (P). nên tiếp tuyến tA tại A của (P) cũng là tiếp tuyến của (C).
Xét điểm
A
a
;
1
2
;
a
2
,
![]()
Ta có hệ điều kiện:
A ∈ ( C ) I A ⊥ t A
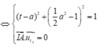
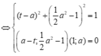
Vậy phương trình đường tròn
![]()
![]()
Diện tích hình phẳng cần tính là
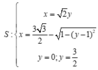
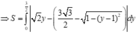
![]()
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho parabol (P):
y
3
m
+
4
−
7
4
x
2
và đường thẳng (d): y 3x – 5. Biết đường thẳng d cắt (P) tại một điểm có tung độ y 1. Tìm m và hoành độ giao điểm còn lại của d và parabol (P) A. m 0; x 2 B.
m
1...
Đọc tiếp
Cho parabol (P): y = 3 m + 4 − 7 4 x 2 và đường thẳng (d): y = 3x – 5. Biết đường thẳng d cắt (P) tại một điểm có tung độ y = 1. Tìm m và hoành độ giao điểm còn lại của d và parabol (P)
A. m = 0; x = 2
B. m = 1 4 ; x = −10
C. m = 2; x = 8
D. m = 0; x = 10
Thay y = 1 vào phương trình đường thẳng d ta được 3x – 5 = 1 ⇔ x = 2
Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (2; 1)
Thay x = 2; y = 1 vào hàm số y = 3 m + 4 − 7 4 x22
ta được: 3 m + 4 − 7 4 .2 2 = 1 ⇔ 3 m + 4 − 7 4 = 1 4
⇔ 3 m + 4 = 2 ⇔ 3m + 4 = 4
⇔ 3m = 0 ⇔ m = 0 ⇒ (P): y = 1 4 x 2
Xét phương trình hoành độ giao điểm của d và (P):
1 4 x 2 = 3 x − 5 ⇔ x2 – 12x + 20 = 0
⇔ (x – 2) (x – 10) = 0 ⇔ x = 2 x = 10
Vậy hoành độ giao điểm còn lại là x = 10
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)

















