Cho hàm số:
\(v:\left\{ {1;2;3;4;5} \right\} \to \mathbb{R}\)
\(n \to {\rm{ }}v\left( n \right) = 2n\)
Tính \(v\left( 1 \right),v\left( 2 \right),v\left( 3 \right),v\left( 4 \right),v\left( 5 \right)\).
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho hàm số \(y = \frac{1}{x}\) và ba điểm \(M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)\). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?
Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta thấy \({x_N} = 0\)=> Điểm N không thuộc đồ thị.
Thay \({x_M} = - 1\) vào ta được: \(y = \frac{1}{{ - 1}} = - 1\)=> Điểm M thuộc đồ thị.
Thay \({x_P} = 2\) vào ta được: \(y = \frac{1}{2} \ne {y_P}\)=> Điểm P không thuộc đồ thị.
Cho hai hàm số \(f\left( x \right) = {x^3} + x\) và \(g\left( x \right) = {x^2} + 1\,\,\left( {x \in \mathbb{R}} \right).\) Hãy cho biết:
a) Hai hàm số \(f\left( x \right),g\left( x \right)\) có liên tục tại \(x = 2\) hay không.
b) Các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại \(x = 2\) hay không.
a) Ta có \(f\left( x \right),g\left( x \right)\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right),g\left( x \right)\) liên tục tại \(x = 2\)
b) \(\begin{array}{l}f\left( x \right) + g\left( x \right) = {x^3} + {x^2} + x + 1\\f\left( x \right) - g\left( x \right) = {x^3} - {x^2} + x - 1\\f\left( x \right).g\left( x \right) = \left( {{x^3} + x} \right)\left( {{x^2} + 1} \right) = {x^5} + 2{x^3} + x\\\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^3} + x}}{{{x^2} + 1}} = \frac{{x\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = x\end{array}\)
Ta có \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \(x = 2\)
Cho \(u = u(x),v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?
A. \(\left( {\frac{u}{v}} \right)' = \frac{{u'}}{{v'}}\) với \(v = v(x) \ne 0,v = v'(x) \ne 0\)
B. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{v}\) với \(v = v(x) \ne 0\)
C. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) với \(v = v(x) \ne 0\)
D. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{v'}}\) với \(v = v(x) \ne 0;\,\,v' = v'(x) \ne 0\)
Cho hàm số \(y=mx+1\left(m\ne0\right)\left(1\right)\)
1) Tìm m để đồ thị hàm số (1) đi qua điểm \(M\left(-1;-1\right)\). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
2) Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng \(y=\left(m^2-2\right)x+2m+3\)
3) Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng \(\dfrac{2}{\sqrt{5}}\).
1) \(y=mx+1\left(m\ne0\right)\left(1\right)\) hay \(mx-y+1=0\)
Để đồ thị hàm số \(\left(1\right)\) đi qua điểm \(M\left(-1;-1\right)\) khi và chỉ khi
\(m.\left(-1\right)+1=-1\)
\(\Leftrightarrow-m=-2\)
\(\Leftrightarrow m=2\)
Vậy hàm số \(\left(1\right):y=2x+1\)
Bạn tự vẽ đồ thị nhé!
2) \(y=\left(m^2-2\right)x+2m+3\left(d\right)\)
Để \(\left(1\right)//\left(d\right)\) khi và chỉ khi
\(\left\{{}\begin{matrix}m^2-2=2\\2m+3\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\2m\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne-1\end{matrix}\right.\) \(\Leftrightarrow m=\pm2\) thỏa đề bài
3) Khoảng cách từ gốc O đến đồ thị hàm số \(\left(1\right)\) là:
\(d\left(O;\left(1\right)\right)=\dfrac{m.0-0+1}{\sqrt[]{2^2+1^2}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow\dfrac{0.m+1}{\sqrt[]{5}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow0m=1\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có giá trị nào của m để thỏa mãn đề bài,
Đáp án:
1. Tìm m để đồ thị hàm số (1) đi qua điểm M (−1;−1). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
Để đồ thị hàm số (1) đi qua điểm M (−1;−1), ta cần có m(−1)+1=−1. Từ đó ta có m=−2.
Với m=−2, đồ thị hàm số (1) là một đường thẳng có hệ số góc -2 và đi qua điểm M (−1;−1). Ta có thể vẽ đồ thị hàm số như sau:
[Image of the graph of y=-2x+1]
2. Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 =
Hai đường thẳng song song khi hệ số góc của chúng bằng nhau. Do đó, ta có m=m2−2. Từ đó ta có m=2.
3. Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5
Khoảng cách từ gốc O đến đồ thị hàm số (1) là khoảng cách từ điểm (0;1) đến đường thẳng y=mx+1. Khoảng cách này được tính theo công thức:
d=|m|
Do đó, ta có d=2552=2.
Từ đó, ta có m=2.
Kết luận:
Giá trị của m để đồ thị hàm số (1) đi qua điểm M (−1;−1) là m=-2. Giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 = là m=2. Giá trị của m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5 là m=2.Lưu ý:
Để giải bài toán 1 và 2, ta có thể thay m=-2 vào hàm số (1) và so sánh với tọa độ của điểm M (−1;−1) hoặc tọa độ của một điểm bất kỳ trên đường thẳng y (m² - 2) x + 2m+3 =. Để giải bài toán 3, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.chúc bạn học tốt
Cảm ơn em đã tham gia hỏi đáp olm.
Trong câu trả lời của Nguyễn Bảo Long là câu coppy chat gpt.
Lần này cô nhắc nhở, lần sau cô xử phạt
Cho hàm số y= \(\frac{\left|x+1\right|+\left|x-1\right|}{\left|x+1\right|-\left|x-1\right|}\)
a) Tìm miền xác định của hàm số
b) Lập bảng biến thiên và vẽ đồ thị hàm số
Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=x\left(x+1\right)^2\left(x^2+2mx+1\right)\) với mọi x thuộc R. Có bao nhiêu số nguyên âm m để hàm số \(g\left(x\right)=f\left(2x+1\right)\) đồng biến trên khoảng (3;5)
Cho đồ thị hàm số \(y = f\left( x \right)\) như Hình 8.
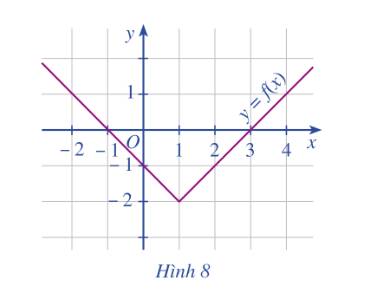
a) Trong các điểm có tọa độ \(\left( {1; - 2} \right),\left( {0;0} \right),\left( {2; - 1} \right)\), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right);f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).
Cho hàm số \(y=\dfrac{1}{2x^2+x-1}\). Hỏi đạo hàm cấp 2019 của hàm số bằng biểu thức nào sau đây?
A. \(\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}-\dfrac{2^{2019}}{\left(2x-1\right)^{2020}}\right)\)
B. \(\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}-\dfrac{2^{2020}}{\left(2x-1\right)^{2020}}\right)\)
C. \(\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}-\dfrac{2}{\left(2x-1\right)^{2020}}\right)\)
D. \(\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}+\dfrac{2}{\left(2x-1\right)^{2020}}\right)\)
\(y=\dfrac{1}{2x^2+x-1}=\dfrac{1}{\left(x+1\right)\left(2x-1\right)}=\dfrac{2}{3}.\dfrac{1}{2x-1}-\dfrac{1}{3}.\dfrac{1}{x+1}\)
\(y'=\dfrac{2}{3}.\dfrac{-2}{\left(2x-1\right)^2}-\dfrac{1}{3}.\dfrac{-1}{\left(x+1\right)^2}=\dfrac{2}{3}.\dfrac{\left(-1\right)^1.2^1.1!}{\left(2x-1\right)^2}-\dfrac{1}{3}.\dfrac{\left(-1\right)^1.1!}{\left(x+1\right)^2}\)
\(y''=\dfrac{2}{3}.\dfrac{\left(-1\right)^2.2^2.2!}{\left(2x-1\right)^3}-\dfrac{1}{3}.\dfrac{\left(-1\right)^2.2!}{\left(x+1\right)^3}\)
\(\Rightarrow y^{\left(n\right)}=\dfrac{2}{3}.\dfrac{\left(-1\right)^n.2^n.n!}{\left(2x-1\right)^{n+1}}-\dfrac{1}{3}.\dfrac{\left(-1\right)^n.n!}{\left(x+1\right)^{n+1}}\)
\(\Rightarrow y^{\left(2019\right)}=\dfrac{2}{3}.\dfrac{\left(-1\right)^{2019}.2^{2019}.2019!}{\left(2x-1\right)^{2020}}-\dfrac{1}{3}.\dfrac{\left(-1\right)^{2019}.2019!}{\left(x+1\right)^{2020}}\)
\(=\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}-\dfrac{2^{2020}}{\left(2x-1\right)^{2020}}\right)\)