Xét ΔABO vuông tại O và ΔDCO vuông tại O có

góc BAO=góc CDO

=>ΔABO đồng dạng với ΔDCO

Xét ΔBCO vuông tại O và ΔADO vuông tại O có

góc OBC=góc OAD

=>ΔBCO đồng dạng với ΔADO

Mọi người giúp với !!

 a, Chắc bạn vẫn còn nhớ phương pháp chứng mình 1 tứ giác là hình chữ nhật bằng cách chứng minh 2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Xét thấy tứ giác ABDC có tính chất như vậy nên nó là hình chữ nhật. 
b,Xét tam giác AHB và tam giác BMA có góc AHb = góc BMA = 90 độ; cạnh AB chung; góc A = góc B (2 góc đáy của tam giác ABO cân tại O). => 2 tam giác này bằng nhau (cạnh huyền, góc nhọn) => BH = AM (cặp cạnh tương ứng). Xét tam giác ABO có AM/AO = BH/BO (do BH = AM và AO = BO). 
=> MH song song với AB (định lý Ta - lét đảo). Mà AB vuông góc với AC nên suy ra HM vuông góc với AC. 
c, Xét tam giác BHA và tam giác DNC có góc H = góc N = 90 độ; AB = CD và góc ABH = góc CDN => 2 tam giác này bằng nhau => BH = ND, tương tự cũng suy ra HN song song với BD (giống phần b). Do MH song song với AB; HN song song với BD => góc MHN = góc ABD = 90 độ (2 góc có cặp cạnh tương ứng song song thì bằng nhau nếu cùng nhọn, cùng tù hoặc có 1 góc vuông trong 2 góc ) => tam giác MHN vuông tại H => tâm đường tròn ngoại tiếp chình là trung điểm cạnh huyền và O chính là nó (hãy tự suy ra dựa vào những phần trên). 
d, Gọi I là tâm đường tròn nội tiếp tam giác ABC vuông tại A, ta có tính chất sau r (bán kính đường tròn nội tiếp) = (AB + AC - BC)/2. Ta sẽ đi chứng minh điều này: Xét tam giác ABC vuông tại A có I là tâm đường tròn nội tiếp. Kẻ IH vuông góc với AB; IK vuông góc với AC và IL vuông góc với BC. => Ta chứng minh được r = AH = AK. BH = BL và CK = LC (hãy tự chứng minh bằng cách nôi A với I; B với I và C với I) => AH + AK = (AB - HB + AC - KC) = (AB + AC - BH - CK) = (AB + AC - BL - LC) = (AB + AC - BC) <=> 2r = (AB + AC - BC) => r = AB + AC - BC)/2 mà R = BC/2 (tính chất trong tam giác vuông) => R + r = AB + AC - BC)/2 + BC/2 = (AB + AC)/2. Mà AB + AC >hoặc= 2 nhân căn bậc 2 (AB.AC) => (AB + AC)/2 >hoặc= căn bậc 2 của(AB.AC) (đpcm)

a) góc A = 90 (1) => BC là đuòng kính => góc BDC = 90 (2) 
AD là đường kính => góc ABD = 90 (3) 
Từ (1),(2),(3) => ABDC là hình chữ nhật (tứ giác có 4 góc vuông) 
b) HM cắt AC tại E 
góc BAH = góc HCA = góc DAC 
(cùng phụ với HAC) 
=> BAH + OAH = OAC + OAH 
góc OAB = góc HAC 
mà góc AMB = góc AHC = 90 
=> góc ABM = góc ACH 
Tứ giác ABHM nội tiếp ( do góc AMB = góc AHB = 90 ) 
=> góc ABM = góc AHM 
=> góc AHM = góc ACH 
mà góc AHM + góc HMC = 90 
=> góc ACH + góc HMC = 90 
=> góc HEC = 90 => HM vuông góc AC 
c) góc AHC -= góc ANC = 90 => Tứ giác AHNC nội tiếp 
=> góc ANH = góc ACH ( nhìn cạnh AH) 
mà góc ACH = góc CAN (do tg OAC cân) => góc ANH = góc CAN => HN // AC 
HM vuông góc AC => HM vuông góc HN => tam giác MHN vuông tại H 
ta có : góc ANH = góc ACH = góc CHN => tam giác OHN cân tại O => OH = ON (4) 
(so le trong) 
góc ACH = góc ANH, góc MHN = góc HEC = 90 => góc HMN = góc EHC => tam giác OHM cân tại O 
=> OH = OM (5) 
Từ (4) và (5) => OM = ON = OH => O cách đều ba điểm M,H,N 
=> Điểm O là tâm đuùong tròn ngoại tiếp tam giác MHN

~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~

 ~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~

~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

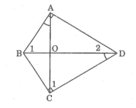
Vì  △ ABO đồng dạng  △ DCO nên:

∠ B 1 = ∠ C 1 (1)

Mà  ∠ C 1 = ∠ C 2  =  ∠ (BCD) =  90 0  (2)

Trong  △ ABD, ta có:  ∠ A = 90 0

Suy ra:  ∠ B 1 = ∠ D 2  =  90 0 (3)

Từ (1), (2) và (3): Suy ra:  ∠ C 2 = ∠ D 2

Xét  △ BCO và  △ ADO, ta có:

∠ C 2 = ∠ D 2  (chứng minh trên)

∠ (BOC) =  ∠ (AOD) (đối đỉnh)

Vậy  △ BOC đồng dạng △ ADO (g.g).

a) Xét ΔABO và ΔDCO có

\(\widehat{BAO}=\widehat{CDO}\)(gt)

\(\widehat{AOB}=\widehat{DOC}\)(hai góc đối đỉnh)

Do đó: ΔABO∼ΔDCO(g-g)

b) Ta có: ΔABO∼ΔDCO(cmt)

⇒\(\dfrac{OB}{OC}=\dfrac{OA}{OD}\)(Các cặp cạnh tương ứng tỉ lệ)

⇔\(\dfrac{OB}{OA}=\dfrac{OC}{OD}\)

Xét ΔBCO và ΔADO có 

\(\dfrac{OB}{OA}=\dfrac{OC}{OD}\)(cmt)

\(\widehat{BOC}=\widehat{AOD}\)(hai góc tương ứng)

Do đó: ΔBCO∼ΔADO(c-g-c)

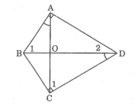
Xét  △ ABO và  △ DCO,ta có:

∠ (BAO) =  ∠ (BDC) (gt)

Hay  ∠ (BAO) =  ∠ (ODC)

∠ (AOB) =  ∠ (DOC) (đối đỉnh)

Vậy  △ ABO đồng dạng  △ DCO (g.g)