Xét ΔABO vuông tại O và ΔDCO vuông tại O có
góc BAO=góc CDO
=>ΔABO đồng dạng với ΔDCO
Xét ΔBCO vuông tại O và ΔADO vuông tại O có
góc OBC=góc OAD
=>ΔBCO đồng dạng với ΔADO
Xét ΔABO vuông tại O và ΔDCO vuông tại O có
góc BAO=góc CDO
=>ΔABO đồng dạng với ΔDCO
Xét ΔBCO vuông tại O và ΔADO vuông tại O có
góc OBC=góc OAD
=>ΔBCO đồng dạng với ΔADO
TỨ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O, góc BOA bằng góc BDC. Chứng minh:
a) tam giác ABO đồng dạng tam giác DCO
b) tam giác BCO đồng dạng tam giác ADO
CHo tứ giác ABCD có góc A = góc C = 90, hai đường chéo AC và BD cắt nhau tại O, góc BAO = góc BDC. CM :
a. tam giác ABO đồng dạng với tam giác DCO
b. tam giác BCO đồng dạng vưới tam giác ADO
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ BCO đồng dạng △ ADO
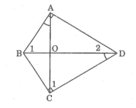
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ ABO đồng dạng △ DCO
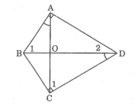
tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, góc ABD= góc ACD. Gọi E là giao điểm của AD và BC. Chứng minh:
a) Tam giác AOB đồng dạng với tam giác DOC.
b) Tam giác AOD đồng dạng với tam giác BOC.
c)EA.ED=EB.EC
Tứ giác ABCD có 2 đường chéo AC và BD cắt nhau tại O, góc ABD= góc ACD. Gọi E là giao điểm của AD và BC
Chứng minh: a) tam giác AOB đồng dạng với tam giác DOC
b) Tam giác AOP đồng dạng với tam giác BOC
c) EA.ED=ED.EC
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại I và góc ABD= góc ACD
a, Chứng minh tam giác AIB đồng dạng với tam giác DIC
b,AI.BC=AD.BI
c, Từ D kẻ tia phân giác DM của tam giác ADC. Tính DM biết AC=5cm, AD=3cm và góc ADC=90 độ
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại I và góc ABD= góc ACD
a, Chứng minh tam giác AIB đồng dạng với tam giác DIC
b,AI.BC=AD.BI
c, Từ D kẻ tia phân giác DM của tam giác ADC. Tính DM biết AC=5cm, AD=3cm và góc ADC=90 độ
Cho hình chữ nhật ABCD (AD <AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .
a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .
b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB = . Từ đó tính
độ dài CH biết AD = 6cm ; AB = 8cm.
c) Gọi K là giao điểm của OE và HC . Chứng minh:
HK /OD=EK/EO, từ đó suy ra: K là trung điểm của HC .
d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy