Các câu hỏi tương tự
Cho tứ giác ABCD có hai góc vuông tại đỉnh A và C , hai đường chéo AC và BD cắt nhau tại O, BAO=BDC
chứng minh tam giác ABO đồng dạng với tam giác DCO
tam giác BCO đồng dạng với tam giác ADO
CHo tứ giác ABCD có góc A = góc C = 90, hai đường chéo AC và BD cắt nhau tại O, góc BAO = góc BDC. CM :
a. tam giác ABO đồng dạng với tam giác DCO
b. tam giác BCO đồng dạng vưới tam giác ADO
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O,
∠
(BAO)
∠
(BDC) .Chứng minh:
△
BCO đồng dạng
△
ADO
Đọc tiếp
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ BCO đồng dạng △ ADO
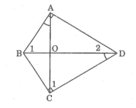
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ ABO đồng dạng △ DCO
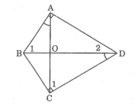
tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, góc ABD= góc ACD. Gọi E là giao điểm của AD và BC. Chứng minh:
a) Tam giác AOB đồng dạng với tam giác DOC.
b) Tam giác AOD đồng dạng với tam giác BOC.
c)EA.ED=EB.EC
Cho tứ giác ABCD có hai đường chéo AC và BD cát nhau tại O. Các đường thẳng AB và CD cắt nhau tại M. Biết AB=7cm, CD=11cm, MA=5cm, MD=4cm. Chứng minh:
Tam giác MAD đồng dạng tam giác MCB
Góc MAC bằng góc MDB
OA.OC bằng OD.OB
tam giác AOD đồng dạng tam giác BOC
Tứ giác ABCD có 2 đường chéo AC và BD cắt nhau tại O, góc ABD= góc ACD. Gọi E là giao điểm của AD và BC
Chứng minh: a) tam giác AOB đồng dạng với tam giác DOC
b) Tam giác AOP đồng dạng với tam giác BOC
c) EA.ED=ED.EC
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại I và góc ABD= góc ACD
a, Chứng minh tam giác AIB đồng dạng với tam giác DIC
b,AI.BC=AD.BI
c, Từ D kẻ tia phân giác DM của tam giác ADC. Tính DM biết AC=5cm, AD=3cm và góc ADC=90 độ
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại I và góc ABD= góc ACD
a, Chứng minh tam giác AIB đồng dạng với tam giác DIC
b,AI.BC=AD.BI
c, Từ D kẻ tia phân giác DM của tam giác ADC. Tính DM biết AC=5cm, AD=3cm và góc ADC=90 độ








