Cho tam giác ABC vuông cân tại C, CA=CB=a. E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc với AE tại H cắt AC tại K.
Chứng minh BE.BC + AC . AK không đổi
Những câu hỏi liên quan
Bài 1:Cho tam giác ABC vuông tại A, AB AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh AK ACBài 2Tam giác ABC vuông tại A có AB AC. Lấy D thuộc cạnh AB, E thuộc cạnh AC sao cho AD AE. Đường thẳng qua D và vuông góc với BE cắt đường thẳng CA ở K. Chứng minh AK ACBài 3Cho tam giác ABC có I là trung điểm AB. Đường thẳng qua I và song song với BC cắt AC ở K. Đường thẳng qua K và song song với AB cắt BC ở H. Chứng minh:a) KH IBb) AK KCc) IH //...
Đọc tiếp
Bài 1:
Cho tam giác ABC vuông tại A, AB = AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh AK = AC
Bài 2
Tam giác ABC vuông tại A có AB = AC. Lấy D thuộc cạnh AB, E thuộc cạnh AC sao cho AD = AE. Đường thẳng qua D và vuông góc với BE cắt đường thẳng CA ở K. Chứng minh AK = AC
Bài 3
Cho tam giác ABC có I là trung điểm AB. Đường thẳng qua I và song song với BC cắt AC ở K. Đường thẳng qua K và song song với AB cắt BC ở H. Chứng minh:
a) KH = IB
b) AK = KC
c) IH // AC
d) H là trung điểm của BC
Cho tam giác giác ABC vuông tại A có AB = AC. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA tại K. Chứng minh rằng AK = AC.
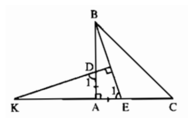
Từ (1) và (2) suy ra AK = AC (điều phải chứng minh ).
Đúng 1
Bình luận (0)
cho tam giác ABC có AB = AC, tia phân giác góc A cắt cạnh BC tại D.
a> chứng minh tam gisc ABD = ACD và AD vuông với BC
b> Qua B kẻ đường thẳng vuông góc với BC, đường thẳng này cắt CA tại E. chứng minh goscAEB = ABE
c> Kẻ AK vuông góc với BE ( K thuộc BE) chứng minhAK = 1/2 BC
+ Xét \(\Delta ABD;\Delta ACD\)có :
AB = AC (gt)
\(\widehat{BAD}=\widehat{CAD}\)( AD là p/g góc A)
AD cạnh chung
=> \(\Delta ABD=\Delta ACD\)(c-g-c)
=> \(\widehat{ADB}=\widehat{ADC}\)( hai góc tương ứng)
Mà \(\widehat{ADB}+\widehat{ADC}=180^o\)( kề bù)
=> \(\widehat{ADB}=\widehat{ADC}=\frac{180^o}{2}=90^o\Rightarrow AD\perp BC\)
+ Vì AD _|_ BC tại D
EB _|_ BC tại B => AD // EB ( q/h vuông góc và song song)
=> \(\hept{\begin{cases}\widehat{AEB}=\widehat{CAD}\\\widehat{ABE}=\widehat{BAD}\end{cases}}\)
Mà \(\widehat{CAD}=\widehat{BAD}\Rightarrow\widehat{AEB}=\widehat{ABE}\)
+ Vì \(\Delta ABD=\Delta ACD\Rightarrow BD=CD\)(2 cạnh t/ứng)
Mà D thuộc BC => BD = 1/2 BC (1)
+ Xét \(\Delta AKB;\Delta BDA\)có :
\(\widehat{K}=\widehat{D}=90^o\left(AK\perp BE;AD\perp BC\right)\)
AB là cạnh chung
\(\widehat{KBA}=\widehat{DAB}\)( so le trong, AD // BE)
=> \(\Delta AKB=\Delta BDA\)( cạnh huyền-góc nhọn)
=> AK = BD ( 2 cạnh t/ứng) (2)
Từ (1),(2) => đpcm
Đúng 0
Bình luận (1)
tam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK KC
Đọc tiếp
tam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD = AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK = KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD = AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK = KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD = AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK = KC
Cho tam giác ABC (AB < AC) vuông tại A. Đường cao AH. Trên cạnh AC lấy điểm E sao cho AH = AE. Qua E kẻ đường thẳng vuông góc với AC cắt BC tại D
a, Chứng minh tam giác AHD = tam giác AED
b, So sánh DH và DC
c, Gọi DE cắt AH tại K. Chứng minh DKC cân tại C
d, Gọi M là trung điểm của KC. Chứng minh ba điểm A, D, M thẳng hàng
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: ΔAHD=ΔAED
=>DH=DE
mà DE<DC
nên DH<DC
c: Xét ΔDHK vuông tại H và ΔDEC vuông tại E có
DH=DE
góc HDK=góc EDC
=>ΔDHK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
d: AH+HK=AK
AE+EC=AC
mà AH=AE và HK=EC
nên AK=AC
mà DK=DC
nên AD là trung trực của KC
mà M là trung điểm của CK
nên A,D,M thẳng hàng
Đúng 2
Bình luận (0)
Bài 1 : Cho xOy có Oz là tia phân giác, M là điểm bất kì thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại a cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D. Chứng minh tam giác AOM bằng tam giác BOM ?Bài 2 : Cho tam giác ABC có góc A 90* và đường phân giác BH (H thuộc AC). Kẻ HM vuông góc với BC (M thuộc BC). Gọi N là giao điểm của AB và MH. Chứng minh tam giác ABH bằng tam giác MBH, tam giác ACE tam giác AKE?Bài 3: Cho tam giác ABC vuông tại C có góc A 60* v...
Đọc tiếp
Bài 1 : Cho xOy có Oz là tia phân giác, M là điểm bất kì thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại a cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D. Chứng minh tam giác AOM bằng tam giác BOM ?
Bài 2 : Cho tam giác ABC có góc A = 90* và đường phân giác BH (H thuộc AC). Kẻ HM vuông góc với BC (M thuộc BC). Gọi N là giao điểm của AB và MH. Chứng minh tam giác ABH bằng tam giác MBH, tam giác ACE= tam giác AKE?
Bài 3: Cho tam giác ABC vuông tại C có góc A = 60* và đường phân gác của góc BAC cắt BC tại E. Kẻ EK vuông góc AB tại K (K thuộc AB). Kẻ BD vuông góc với AE tại D (D thuộc AE). Chứng minh tam giác ACE = tam giác AKE
Bài 4: Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E. Kẻ EH vuông góc BC tại H (H thuộc BC). Chứng minh tam giác ABE = tam giác HBE ?
cho tam giác ABC vuông tại A có AB<AC lấy E thuộc CB sao cho CA=CE qua E kẻ đường vuông góc với BC cắt AB tại D a, chứng minh CD vuông với AE b, lấy F thuộc tia đối của AC sao cho AF=EB chứng minh 3 điểm EDF thẳng hàng
a: Xét ΔCAD vuông tại A và ΔCED vuông tại E có
CD chung
CA=CE
=>ΔCAD=ΔCED
=>CA=CE và DA=DE
=>CD là trung trực của AE
=>CD vuông góc AE
b: Xét ΔDAF vuông tại A và ΔDEB vuông tại E có
DA=DE
AF=EB
=>ΔDAF=ΔDEB
=>góc ADF=góc EDB
=>góc ADF+góc ADE=180 độ
=>E,D,F thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ tia phân giác CD (D thuộc AB). Qua D vẽ đường thẳng vuông góc với CD, cắt CB tại F và CA tại K. Ddường thẳng kẻ qua D và // BC cắt AC tại E. Phân giác của gọc BAC cắt DE tại M. Chứng minh rằng:
a) Tam giác CDF và tam giác CDK bằng nhau.
b) Các tam giác DEC và DEK là tam giác cân.
c) CF = 2BD.
d) MD = 1/4CF.
a: Xét ΔCDF vuông tại D và ΔCDK vuông tại D có
CD chung
góc FCD=góc KCD
=>ΔCDF=ΔCDK
b: Xét ΔEDC có góc EDC=góc ECD
nên ΔECD cân tại E
=>EC=ED
=>góc ECD=góc EDC
=>góc EDK=góc EKD
=>ΔKED cân tại E
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAC
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang