 Giải chi tiết
Giải chi tiết

Những câu hỏi liên quan
4700cm3=.....? ko cần giải chỉ tiết chỉ cần nói kết quả thôi
Xem thêm câu trả lời
Giúp em giải chỉ tiết ạ
7C pollutants( những nguồn gây ô nhiễm)
8 B ( the thường đứng trước danh từ)
9A( tính - danh)
10A result in = lead to: gây ra ; dẫn đến
Đúng 1
Bình luận (0)
Giúp em giải chi tiết câu 19, 20 22 chỉ ra giải thích
19.
\(y'=\dfrac{\left(x^2+3x-4\right)'}{2\sqrt{x^2+3x-4}}=\dfrac{2x+3}{2\sqrt{x^2+3x-4}}\)
20.
\(BC||AD\Rightarrow\) góc giữa BC và SD bằng góc giữa AD và SD
\(\Rightarrow\) Góc giữa BC và SD là góc \(\widehat{SDA}\)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{a}{a}=1\Rightarrow\widehat{SDA}=45^0\)
22.
B là khẳng định sai
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp MB\) ; \(BC\perp SB\) ; \(BC\perp SA\)
Đúng 0
Bình luận (0)
Cho em xin chỉ tiết giải ạ 
Lời giải:
a. Sau 2 năm thu được:
$100(1+\frac{0,5}{100})^{24}=112,72$ (triệu đồng)
b.
Giả sử sau $n$ tháng thì rút ra được gốc lẫn lãi là 300 triệu
$100(1+0,005)^n=300$
$1,005^n=3$
$n=\log_{1,005}3=220,3$ (tháng)
Vậy sau ít nhất 221 tháng thì người đó rút được 300 triệu. Đổi 221 tháng thành 18 năm 5 tháng
Đáp án C.
Đúng 1
Bình luận (1)
Chỉ cần 26, giải chi tiết nhá 
Do \(u\) nhanh pha hơn \(i\) là \(\dfrac{\text{π }}{6}rad\) nên mạch gồm \(L\) và \(R\)
Có:
\(\tan \dfrac{\text{π }}{6}=\dfrac{Z_L}{R}\Rightarrow\dfrac{Z_L}{R}=\dfrac{\sqrt{3}}{3}\Rightarrow R=\sqrt{3}Z_L\)
\(Z=\dfrac{U}{I}=\dfrac{200}{2}=100\Rightarrow R^2+Z_L^2=100^2\)
\(\Rightarrow\left\{{}\begin{matrix}Z_L=50\Omega\Rightarrow L=\dfrac{1}{2\text{π }}\\R=50\sqrt{3}\Omega\end{matrix}\right.H\)
Đúng 2
Bình luận (0)
Giúp e giải chỉ tiết câu 7 này đi ạ mình giải k ra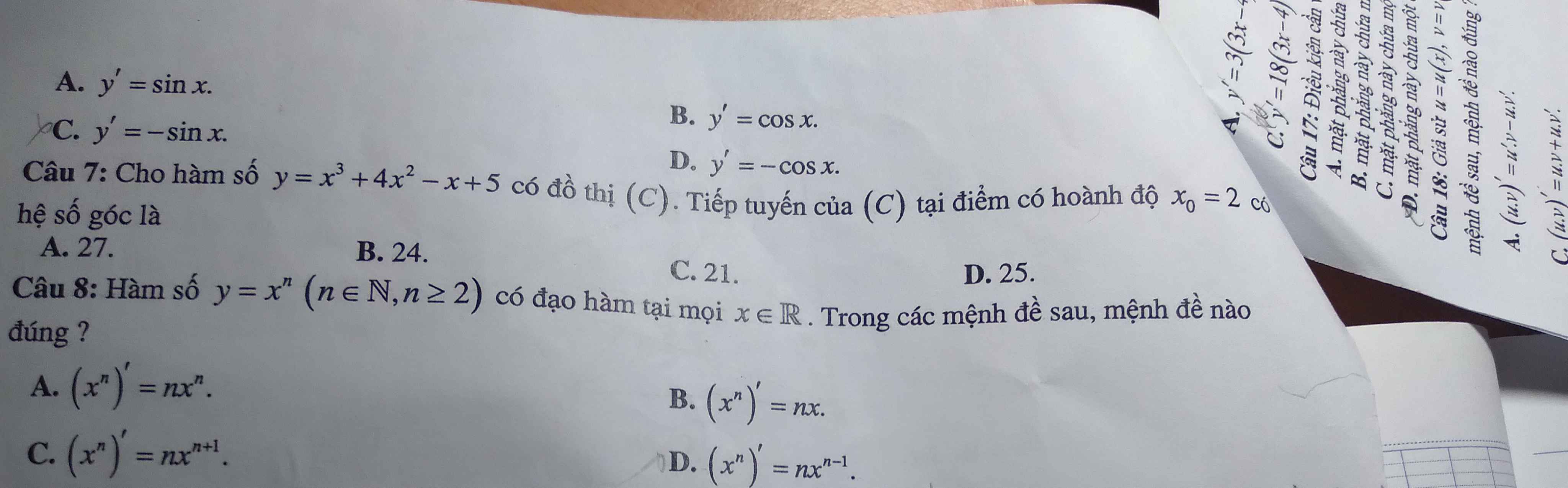
7.
\(y'=3x^2+8x-1\)
\(\Rightarrow y'\left(2\right)=3.2^2+8.2-1=27\)
Đúng 0
Bình luận (0)
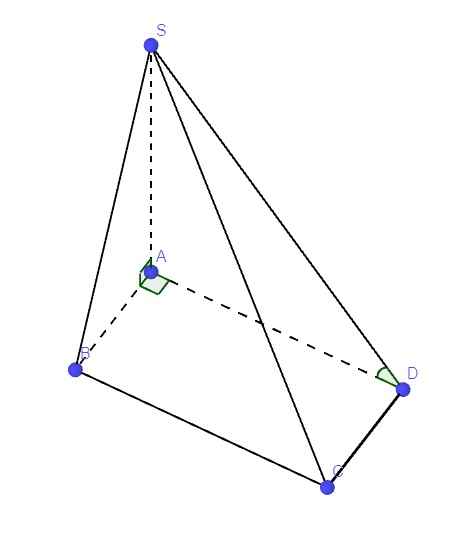
Giúp e giải chỉ tiết đi mn ơi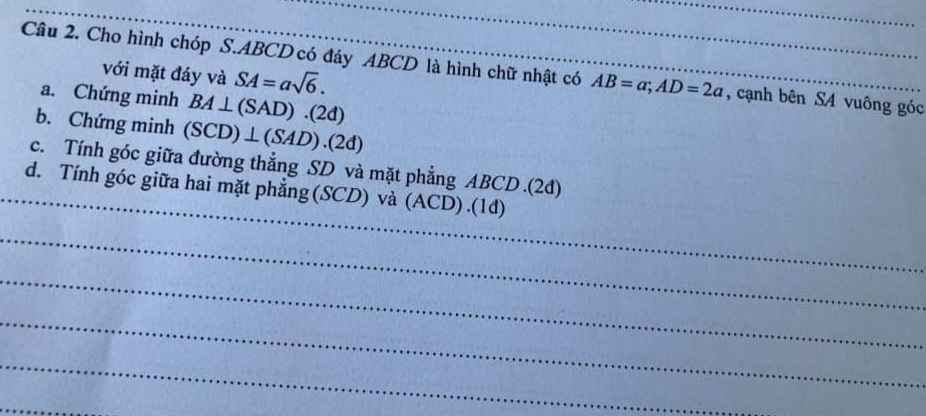
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
b.
Ta có \(CD||AB\) (do ABCD là hcn)
Mà \(AB\perp\left(SAD\right)\Rightarrow CD\perp\left(SAD\right)\)
Lại có \(CD\in\left(SCD\right)\)
\(\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SDA}\approx50^046'\)
d.
Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp\left(ACD\right)\)
Mà \(SA\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(ACD\right)\) (1)
Theo câu b ta có: \(\left(SAD\right)\perp\left(SCD\right)\) (2)
(1);(2) \(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ACD)
Theo câu c ta có: \(\widehat{SDA}=50^046'\)
Đúng 1
Bình luận (0)
chỉ cần đ/án ko cần giải chi tiết
Câu 3: D
Câu 4: C
Câu 5: B
Câu 6: C
Đúng 0
Bình luận (0)
chỉ cần đáp án ko cần giải chi tiết
Câu 1: D
Câu 2: B
Câu 3: C
Câu 4: C
Câu 5: B
Câu 6: a. Đ b. S
Đúng 1
Bình luận (0)
chỉ cần đáp án ko cần giải chi tiết