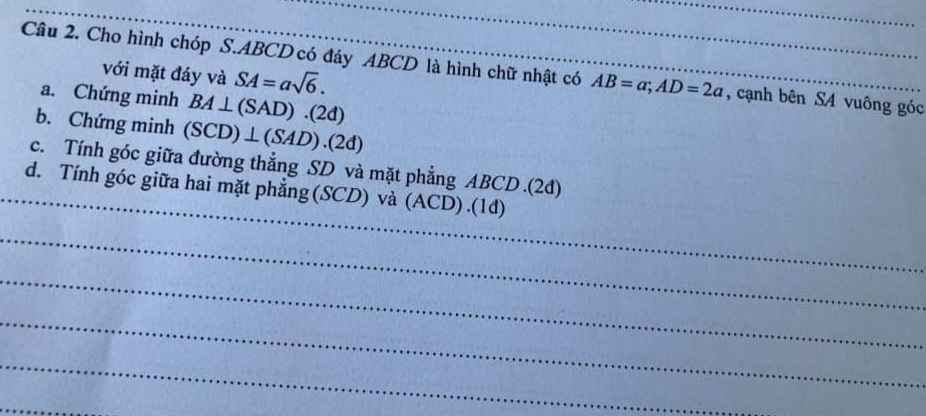a.
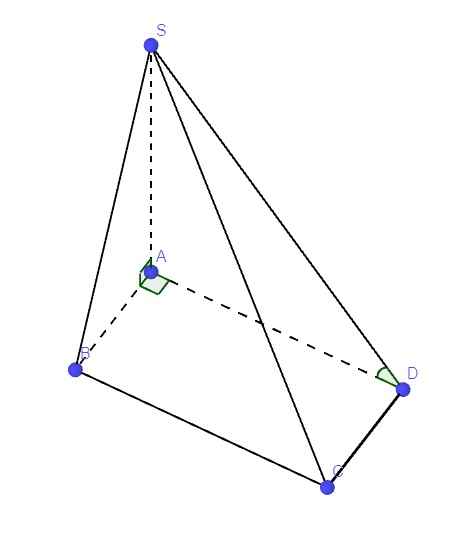
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
b.
Ta có \(CD||AB\) (do ABCD là hcn)
Mà \(AB\perp\left(SAD\right)\Rightarrow CD\perp\left(SAD\right)\)
Lại có \(CD\in\left(SCD\right)\)
\(\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SDA}\approx50^046'\)
d.
Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp\left(ACD\right)\)
Mà \(SA\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(ACD\right)\) (1)
Theo câu b ta có: \(\left(SAD\right)\perp\left(SCD\right)\) (2)
(1);(2) \(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ACD)
Theo câu c ta có: \(\widehat{SDA}=50^046'\)