x4−2x2−3=0

Những câu hỏi liên quan
Phương trình − x 4 + 3 − 2 x 2 = 0 có:
A. 1 nghiệm
B. 2 nghiệm
C. 3 nghiệm
D. 4 nghiệm
Ta có:
− x 4 + 3 − 2 x 2 = 0 ⇔ x 2 − x 2 + 3 − 2 = 0
⇔ x 2 = 0 x 2 = 3 − 2 ( V N ) ⇔ x 2 = 0 ⇔ x = 0
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Giải phương trình x 4 − 2 x 2 − 3 = 0
Cách 1:
x 4 − 2 x 2 − 3 = 0 ⇔ x 4 − 3 x 2 + x 2 − 3 = 0 ⇔ ( x 2 − 3 ) ( x 2 + 1 ) = 0 ⇔ x 2 − 3 = 0 x 2 + 1 = 0 ⇔ x = ± 3 V n ( x 2 ≥ 0 ⇒ x 2 + 1 > 0 )
Vây phương trình có tập nghiệm S = − 3 ; 3
Cách 2: Đặt t=x2 ( t ≥ 0 ) ta có phương trình t2-2t-3=0 (2)
Ta có a-b+c=1+2-3=0 nên phương trình (2) có 2 nghiệm t1=-1(loại);t2=3(nhận)
Với t2=3 ⇔ x 2 = 3 ⇔ x = ± 3
Vậy phương trình có tập nghiệm S = − 3 ; 3
Đúng 0
Bình luận (0)
x4−2x2−30 Phương trình trùng phương
Đọc tiếp
x4−2x2−3=0
Phương trình trùng phương
Đặt \(x^2=t\) \(\left(t\ge0\right)\)
\(\Rightarrow t^2-2t-3=0\\ \Leftrightarrow\Delta=\left(-2\right)^2-4.1.\left(-3\right)=16\\ \Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{2+\sqrt{16}}{2.1}=3\\t_2=\dfrac{2-\sqrt{16}}{2}=-1\end{matrix}\right.\)
\(\Rightarrow t=3\) vì \(t\ge0\)
\(\Rightarrow x^2=3\\ \Rightarrow\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\)
Đúng 2
Bình luận (0)
Đặt t = x² (t ≥ 0)
Phương trình tương đương:
t² - 2t - 3 = 0
Ta có: a - b + c = 1 - (-2) - 3 = 0
Phương trình có hai nghiệm:
t₁ = -1 (loại)
t₂ = 3 (nhận)
Với t₂ = 3
⇔ x² = 3
⇔ x = √3; x = -√3
Vậy S = {-√3; √3}
Đúng 1
Bình luận (0)
Tổng nghiệm của phương trình x4+2x2-3=0 bằng
A.-2 B.-1 C.0 D.-3
\(x^4+2x^2-3=0\Leftrightarrow x^4+3x^2-x^2-3=0\)
\(\Leftrightarrow x^2\left(x+3\right)-\left(x^2+3\right)=0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-3\left(vn\right)\\x^2=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow-1+1=0\)
Đúng 1
Bình luận (0)
Giải phương trình trùng phương x4+2x2-3=0
\(x^4+2x^2-3=0\)\(\Leftrightarrow\left(x^4+2x^2+1\right)-4=0\Leftrightarrow\left(x^2+1\right)^2-2^2=0\Leftrightarrow\left(x^2-1\right)\left(x^2+3\right)=0\Leftrightarrow x^2-1=0\Leftrightarrow x=\pm1\)
Đúng 0
Bình luận (0)
Đặt t = x2 ( t ≥ 0 )
pt đã cho trở thành t2 + 2t - 3 = 0
Xét pt bậc 2 ẩn t có a + b + c = 0 nên pt có hai nghiệm t1 = 1(tm) ; t2 = c/a = -3 (ktm)
=> x2 = 1 <=> x = ±1
Vậy ...
Cho
f
x
x
4
−
2
x
2
−
3
. Tập nghiệm của bất phương trình:
f
x
0
là: A.
S
−
1
;
0
∪
1
;
+
∞...
Đọc tiếp
Cho f x = x 4 − 2 x 2 − 3 . Tập nghiệm của bất phương trình: f ' x > 0 là:
A. S = − 1 ; 0 ∪ 1 ; + ∞
B. S = 1 ; + ∞
C. S = − 1 ; 0
D. S = − 1 ; + ∞
Đáp án A
Ta có:
f ' x = 4 x 3 − 4 x > 0 ⇔ x − 1 x x + 1 > 0 ⇔ x > 1 − 1 < x < 0
Đúng 0
Bình luận (0)
Giá trị lớn nhất của hàm số y = - x 4 + 2 x 2 + 2 trên [0; 3] là
A. -61
B. 3
C. 61
D. 2
Đáp án B
Ta có: ![]() .
.
Cho ![]()
![]()
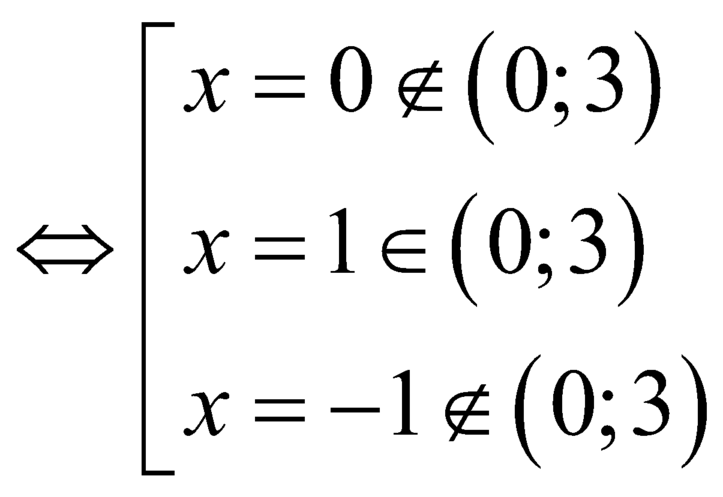 .
.
![]() ;
; ![]() ;
; ![]() .
.
Vậy giá trị lớn nhất của hàm số là 3
Đúng 0
Bình luận (0)
Biện luận theo tham số m số ngiệm của phương trình x4 - 2x2 - m + 3 = 0
x4 - 2x2 - m + 3 = 0 \(\Rightarrow\) x4 - 2x2 + 3 = m.
Gọi f(x) = x4 - 2x2 + 3, D=R.
f'(x) = 4x3 - 4x = 0 \(\Rightarrow\) Hoặc x=0 hoặc x=1 hoặc x=-1.
Bảng biến thiên
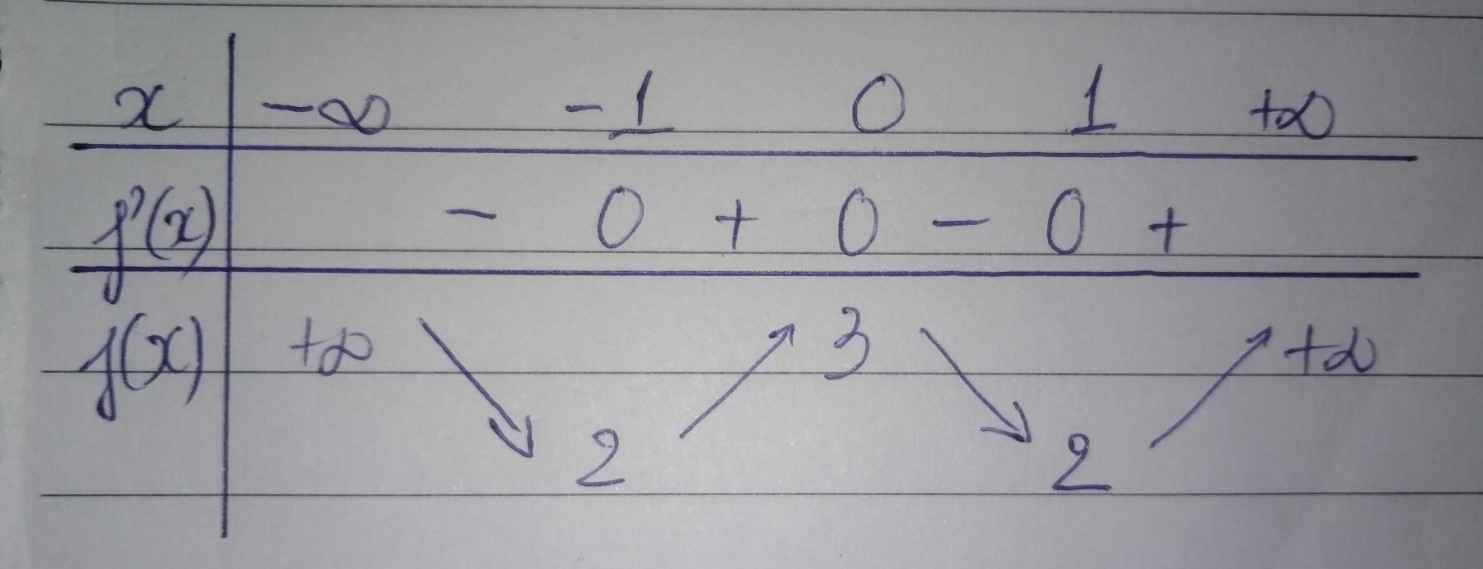
Với m<2, phương trình đã cho vô nghiệm.
Với m=2 hoặc m>3, phương trình đã cho có hai nghiệm đối nhau.
Với m=3, phương trình đã cho có ba nghiệm phân biệt.
Với 2<m<3, phương trình đã cho có bốn nghiệm phân biệt.
Đúng 1
Bình luận (0)
Tìm m để phương trình
x
4
-
2
x
2
+
3
–
m
2
+
2
m
0
có đúng ba nghiệm phân biệt A. m -1 B. m 3 C. -1 m 3 D. Cả A và B
Đọc tiếp
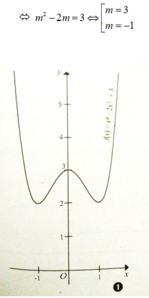
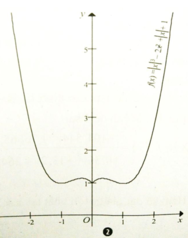
Tìm m để phương trình x 4 - 2 x 2 + 3 – m 2 + 2 m = 0 có đúng ba nghiệm phân biệt
A. m = -1
B. m = 3
C. -1 < m < 3
D. Cả A và B
Chọn D
Xét hàm số y = x 4 - 2 x 2 + 3 ( C )
Đồ thị có dạng như hình (1)
x 4 - 2 x 2 + 3 - m 2 + 2 m = 0 có đúng ba nghiệm phân biệt <=> Đường thẳng y = m 2 + 2 m cắt đồ thị C tại ba điểm phân biệt
Đúng 0
Bình luận (0)















