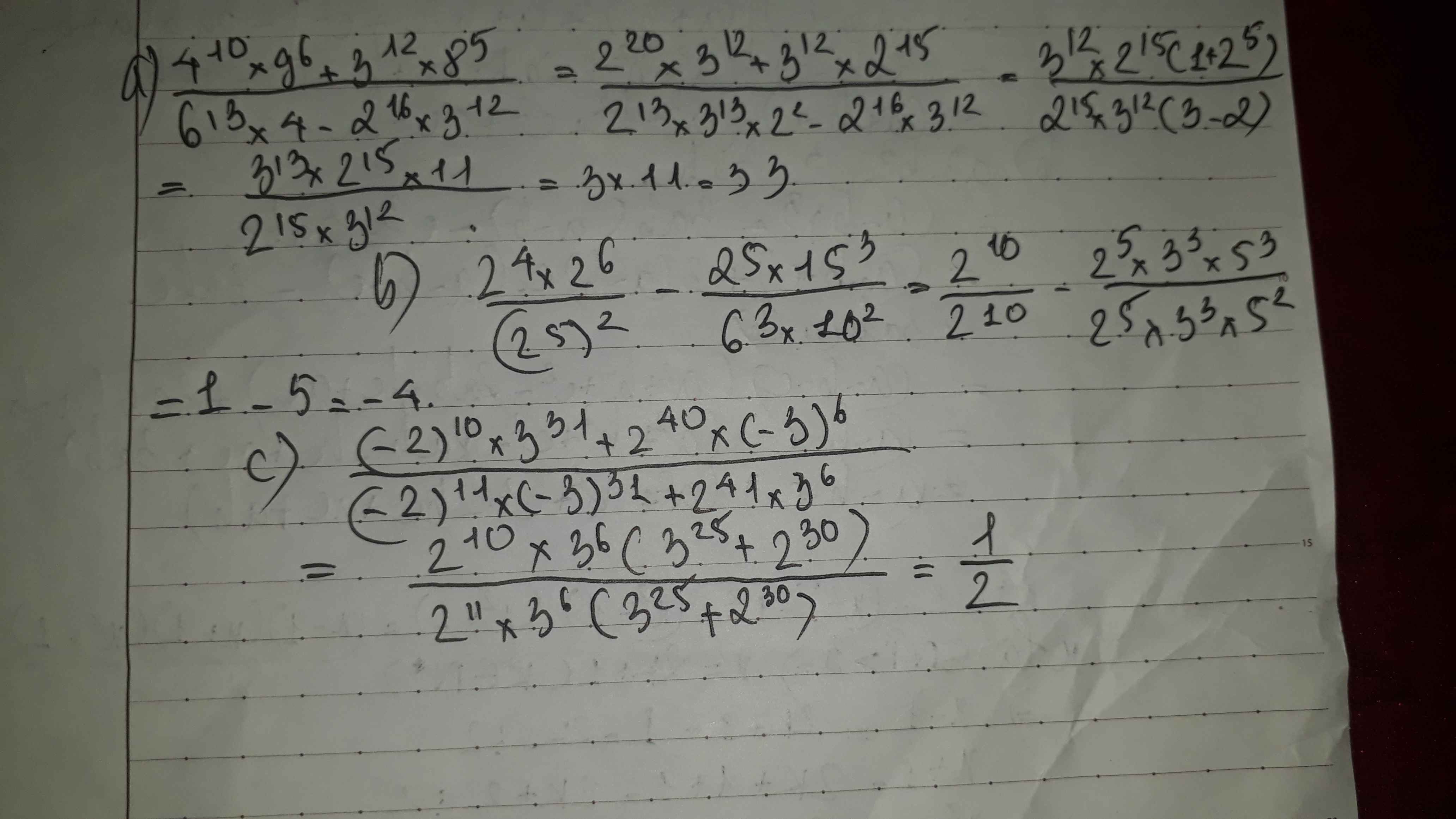\(B=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{9\times10}\)

Những câu hỏi liên quan
chứng minh
M=\(\dfrac{3}{1^2\times2^2}+\dfrac{5}{2^2\times3^2}+\dfrac{7}{3^2\times4^2}+.......+\dfrac{19}{9^2\times10^2}< 1\)
\(M=\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+\dfrac{7}{3^2.4^2}+...+\dfrac{19}{9^2.10^2}\)
\(M=\dfrac{2^2-1^2}{1^2.2^2}+\dfrac{3^2-2^2}{2^2.3^2}+\dfrac{4^2-3^2}{3^2.4^2}+...+\dfrac{10^2-9^2}{9^2.10^2}\)
\(M=1-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+\dfrac{1}{3^2}-\dfrac{1}{4^2}+...+\dfrac{1}{9^2}-\dfrac{1}{10^2}\)
\(M=1-\dfrac{1}{10^2}< 1\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Tính giá trị biểu thức:
B=\(\dfrac{5}{1\times2}+\dfrac{13}{2\times3}+\dfrac{25}{3\times4}+\dfrac{41}{4\times5}+...+\dfrac{181}{9\times10}\)
\(B=\dfrac{5}{1.2}+\dfrac{13}{2.3}+\dfrac{25}{3.4}+\dfrac{41}{4.5}+...+\dfrac{181}{9.10}\)
\(=\left(\dfrac{1}{1.2}+\dfrac{4}{1.2}\right)+\left(\dfrac{1}{2.3}+\dfrac{12}{2.3}\right)+\left(\dfrac{1}{3.4}+\dfrac{24}{3.4}\right)+...+\left(\dfrac{1}{9.10}+\dfrac{180}{9.10}\right)\)
\(\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\right)+\left(\dfrac{4}{1.2}+\dfrac{12}{2.3}+...+\dfrac{180}{9.10}\right)\)
\(=\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)+\left(2+2+...+2\right)\)
\(=1-\dfrac{1}{10}+\left(2.9\right)\)
\(=1-\dfrac{1}{10}+18\)
\(=\dfrac{9}{10}+18\)
\(=18\dfrac{9}{10}\)
Đúng 0
Bình luận (0)
\(D=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+....+\dfrac{1}{2022\times2023}\)
D=1/1-1/2+1/2-1/3+1/3-1/4+.....+1/2022-1/2023
=1-1/2023=2022/2023
Đúng 0
Bình luận (0)
1/1x2+1/2x3+1/3x4+...+1/2022x2023
=1-1/2+1/2-1/3+1/3-1/4+....+1/2022-1/2023
=1-1/2023=2022/2023
...
Đúng 0
Bình luận (0)
a)\(\left(\dfrac{17}{10}+7-8,7\right)\div\left(\dfrac{23}{4}-\dfrac{11}{4}+\dfrac{9}{25}\right)\times\left(12,98\times0,25\right)+12,5\)
b)\(1\dfrac{2}{24}\times5\dfrac{2}{5}\times2\times3\dfrac{7}{9}\times2\times\dfrac{2}{17}\)
a: \(=\left(\dfrac{17}{10}+\dfrac{70}{10}-\dfrac{87}{10}\right):\left(\dfrac{23}{4}-\dfrac{11}{4}+\dfrac{9}{25}\right)\cdot\left(12,98\cdot0,25\right)+12,5\)
\(=0:\left(3+\dfrac{9}{25}\right)\cdot\left(12,98+0,25\right)+12,5\)
=12,5
b: \(=\dfrac{13}{12}\cdot\dfrac{27}{5}\cdot2\cdot\dfrac{34}{9}\cdot2\cdot\dfrac{2}{17}\)
\(=\dfrac{13}{12}\cdot2\cdot\dfrac{27}{5}\cdot\dfrac{34}{9}\cdot\dfrac{4}{17}\)
\(=\dfrac{13}{6}\cdot\dfrac{27}{5}\cdot\dfrac{8}{9}=\dfrac{8}{6}\cdot3\cdot\dfrac{13}{5}=4\cdot\dfrac{13}{5}=\dfrac{52}{5}\)
Đúng 0
Bình luận (0)
\(\dfrac{2}{1\times2\times3}+\dfrac{2}{2\times3\times4}+\dfrac{2}{3\times4\times5}+...+\dfrac{2}{48\times49\times50}\)
\(\dfrac{2}{1\times2\times3}+\dfrac{2}{2\times3\times4}+\dfrac{2}{3\times4\times5}+...+\dfrac{2}{48\times49\times50}\)
\(=\dfrac{1}{1\times2}-\dfrac{1}{2\times3}+\dfrac{1}{2\times3}-\dfrac{1}{3\times4}+\dfrac{1}{3\times4}-\dfrac{1}{4\times5}+...+\dfrac{1}{48\times49}-\dfrac{1}{49\times50}\)
\(=\dfrac{1}{1\times2}-\dfrac{1}{49\times50}\)
\(=\dfrac{1}{2}-\dfrac{1}{2450}\)
\(=\dfrac{612}{1225}\)
\(\text{#}Toru\)
Đúng 2
Bình luận (0)
\(A=\frac{3}{1\times1\times2\times2}+\frac{5}{2\times2\times3\times3}+...+\frac{19}{9\times9\times10\times10}\)
\(\dfrac{4^{10}\times9^6+3^{12}\times8^5}{6^{13}\times4-2^{16}\times3^{12}}\)
\(\dfrac{2^4\times2^6}{\left(2^5\right)^2}-\dfrac{2^5\times15^3}{6^3\times10^2}\)
\(\dfrac{\left(-2\right)^{10}\times3^{31}+2^{40}\times\left(-3\right)^6}{\left(-2\right)^{11}\times\left(-3\right)^{31}+2^{41}\times3^6}\)
giải chi tiết giúp mình nhé
Tính bằng cách hợp lí :
a , dfrac{1}{15}+dfrac{9}{10}+dfrac{14}{15}-dfrac{11}{9}-dfrac{20}{10}+dfrac{1}{157}
b , dfrac{1}{5}-dfrac{-1}{3}+dfrac{-1}{5}-dfrac{2}{6}
c , dfrac{2}{1times3}+dfrac{2}{3times5}+...+dfrac{2}{2015times2017}
d , dfrac{5}{1times3}+dfrac{5}{3times5}+...+dfrac{5}{2015times2017}
e , dfrac{1}{1times2}+dfrac{1}{3times4}+...+dfrac{1}{2016times2017}
Đọc tiếp
Tính bằng cách hợp lí :
a , \(\dfrac{1}{15}+\dfrac{9}{10}+\dfrac{14}{15}-\dfrac{11}{9}-\dfrac{20}{10}+\dfrac{1}{157}\)
b , \(\dfrac{1}{5}-\dfrac{-1}{3}+\dfrac{-1}{5}-\dfrac{2}{6}\)
c , \(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+...+\dfrac{2}{2015\times2017}\)
d , \(\dfrac{5}{1\times3}+\dfrac{5}{3\times5}+...+\dfrac{5}{2015\times2017}\)
e , \(\dfrac{1}{1\times2}+\dfrac{1}{3\times4}+...+\dfrac{1}{2016\times2017}\)
a: \(=\left(\dfrac{1}{15}+\dfrac{14}{15}\right)+\left(\dfrac{9}{10}-2-\dfrac{11}{9}\right)+\dfrac{1}{157}\)
\(=1+\dfrac{1}{157}+\dfrac{81-180-110}{90}\)
\(=\dfrac{158}{157}+\dfrac{-209}{90}\simeq-1.315\)
b: \(=\dfrac{1}{5}+\dfrac{1}{3}-\dfrac{1}{5}-\dfrac{2}{6}\)
=1/3-1/3
=0
c: \(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2015\cdot2017}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2015}-\dfrac{1}{2017}\)
=2016/2017
Đúng 0
Bình luận (0)
Số?a) dfrac{2}{5}dfrac{2times3}{5times3}dfrac{?}{?} dfrac{4}{7}dfrac{4times2}{7times2}dfrac{?}{?} dfrac{13}{54}dfrac{13times3}{54times3}dfrac{?}{?}b) dfrac{8}{20}dfrac{8:4}{20:4}dfrac{?}{?} dfrac{10}{16}dfrac{10:2}{16:2}dfrac{?}{?} dfrac{25}{65}dfrac{25:5}{65:5}dfrac{?}{?}
Đọc tiếp
Số?
a) \(\dfrac{2}{5}=\dfrac{2\times3}{5\times3}=\dfrac{?}{?}\) \(\dfrac{4}{7}=\dfrac{4\times2}{7\times2}=\dfrac{?}{?}\) \(\dfrac{13}{54}=\dfrac{13\times3}{54\times3}=\dfrac{?}{?}\)
b) \(\dfrac{8}{20}=\dfrac{8:4}{20:4}=\dfrac{?}{?}\) \(\dfrac{10}{16}=\dfrac{10:2}{16:2}=\dfrac{?}{?}\) \(\dfrac{25}{65}=\dfrac{25:5}{65:5}=\dfrac{?}{?}\)
a) \(\dfrac{2}{5}=\dfrac{2\times3}{5\times3}=\dfrac{6}{15}=\dfrac{2}{5}\)
\(\dfrac{4}{7}=\dfrac{4\times2}{7\times2}=\dfrac{8}{14}=\dfrac{4}{7}\)
\(\dfrac{13}{54}=\dfrac{13\times3}{54\times3}=\dfrac{39}{162}=\dfrac{13}{54}\)
b) \(\dfrac{8}{20}=\dfrac{8:4}{20:4}=\dfrac{2}{5}\)
\(\dfrac{10}{16}=\dfrac{10:2}{16:2}=\dfrac{5}{8}\)
\(\dfrac{25}{65}=\dfrac{25:5}{65:5}=\dfrac{5}{13}\)
Đúng 1
Bình luận (0)