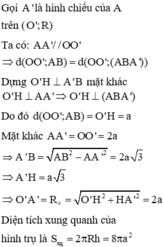trên hình tròn (O;R)biết độ dài một cung tròn 30 độ là π(cm ) thì diện tích một hình quạt tròn cung 60 độ là ???

Những câu hỏi liên quan
Câu 59: Trên hình bên, ta có đường tròn (O; R)A. Điểm O cách mọi điểm trên đường tròn một khoảng RB. Điểm O cách mọi điểm trên hình tròn một khoảng R O R C. Điểm O nằm trên đường tròn D. Chỉ có câu C đúngCâu 60: Gọi S1 là diện tích hình tròn bán kính R1 1 cmS2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:A. S2 2S1 B. S2 S1 C. S2 4S1 ...
Đọc tiếp
Câu 59: Trên hình bên, ta có đường tròn (O; R)
A. Điểm O cách mọi điểm trên đường tròn một khoảng R
B. Điểm O cách mọi điểm trên hình tròn một khoảng R
C. Điểm O nằm trên đường tròn
D. Chỉ có câu C đúng
Câu 60: Gọi S1 là diện tích hình tròn bán kính R1 = 1 cm
S2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:
A. S2 = 2S1 B. S2 = S1 C. S2 = 4S1 D. S2 = 3S1
Cho hình trụ có hai đường tròn đáy là (O) và (O). Gọi A trên đường tròn ( O) và B trên đường tròn (O) sao cho AB 4a. Biết khoảng cách từ đường thẳng AB đến trục của hình trụ a là OO2a. Tính diện tích xung quanh của hình trụ đã cho A. 42πa2 B. 8a2 C. 16πa2 D. 8πa2
Đọc tiếp
Cho hình trụ có hai đường tròn đáy là (O) và (O'). Gọi A trên đường tròn ( O) và B trên đường tròn (O') sao cho AB = 4a. Biết khoảng cách từ đường thẳng AB đến trục của hình trụ a là OO'=2a. Tính diện tích xung quanh của hình trụ đã cho
A. 42πa2
B. 8a2
C. 16πa2
D. 8πa2
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng
a
2
. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O sao cho AB 2a. Tính thể tích của khối tứ diện OO′B′A. A.
a
3
3
2
B.
a
3...
Đọc tiếp
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng a 2 . Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O' sao cho AB' = 2a. Tính thể tích của khối tứ diện OO′B′A.
A. a 3 3 2
B. a 3 2 12
C. a 3 2 6
D. a 3 6
Cho hình trụ có các đáy là 2 hình tròn tâm O và O, bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB2a. Thể tích khối tứ diện OOAB theo a là A.
V
3
a
3
8
B.
V
3...
Đọc tiếp
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB=2a. Thể tích khối tứ diện OO'AB theo a là
A. V = 3 a 3 8
B. V = 3 a 3 4 .
C. V = 3 a 3 6 .
D. V = 3 a 3 12 .
Cho hình nón tròn xoay (N) có đỉnh S và đáy là hình tròn tâm O bán kính r nằm trên mặt phẳng (P) đường cao SOh Điểm O’ thay đổi trên đoạn SO sao cho SO’x (0xh). Hình trụ tròn xoay (T) có đáy thứ nhất là hình tròn tâm O bán kính r’ (0r’r) nằm trên mặt phẳng (P), đáy thứ hai là hình tròn tâm O’ bán kính r’ nằm trên mặt phẳng (Q), (Q) vuông góc với SO tại O’ (đường tròn đáy thứ hai của (T) là giao tuyến của (Q) với mặt xung quanh của (N). Hãy xác định giá trị của x để thể tích phần không gian nằm p...
Đọc tiếp
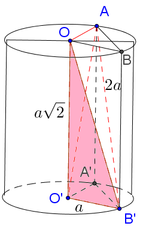
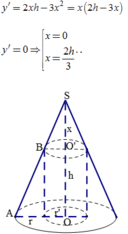
Cho hình nón tròn xoay (N) có đỉnh S và đáy là hình tròn tâm O bán kính r nằm trên mặt phẳng (P) đường cao SO=h Điểm O’ thay đổi trên đoạn SO sao cho SO’=x (0<x<h). Hình trụ tròn xoay (T) có đáy thứ nhất là hình tròn tâm O bán kính r’ (0<r’<r) nằm trên mặt phẳng (P), đáy thứ hai là hình tròn tâm O’ bán kính r’ nằm trên mặt phẳng (Q), (Q) vuông góc với SO tại O’ (đường tròn đáy thứ hai của (T) là giao tuyến của (Q) với mặt xung quanh của (N). Hãy xác định giá trị của x để thể tích phần không gian nằm phía trong (N) nhưng phía ngoài của (T) đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
1. Cho đường tròn (O). Trên đường tròn đó lấy ngẫu nhiên 3 điểm A, B, C. Tính xác suất để \(\Delta ABC\) chứa tâm O của đường tròn.
2. Cho hình cầu tâm (O). Trên mặt hình cầu lấy ngẫu nhiên 4 điểm A, B, C, D. Tính xác suất để hình tứ diện ABCD chứa tâm O của hình cầu.
1. Kẻ đường kính chứa 1 trong 3 điểm A,B,C bất kỳ của (O)
Tam giác ABC chứa tâm O <=>
(*) Có nhiều nhất 2 điểm nằm
trên nửa đường tròn (O) có đường kính như trên , không nhận
cạnh nào là đường kính
(*) ABC là tam giác vuông
Nhận thấy khi tam giác ABC nội tiếp (O) thì A,B,C có 3 trường hợp:
TH1 : 3 điểm cùng nằm trên nửa (O ; DE/2) , không có cạnh nào là đường kính
TH2 : 2 điểm nằm trên nửa (O ; DE/2) ; 1 điểm trên nửa (O) còn lại
TH3 : Tam giác vuông
Biến cố A : " Tam giác ABC chứa tâm O"
=> P(A) = \(\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Trên hình vẽ ta có đường tròn tâm O, bán kính 10cm, tứ giác OABC là hình vuông với A và C nằm trên đường tròn. Tìm phần diện tích của hình vuông nằm ngoài đường tròn.
đúng ghi Đ , sai ghi S :
a, điểm a ở trong hình tròn tâm O.
b, điểm a ở trên đường tròn tâm O.
c, điểm b ở trên đường tròn tâm O .
d, điểm c ở ngoài hình tròn tâm O.
ai nhanh mình tik.
Xin hình đi bạn ơi ! Không có hình thì làm kiểu j ?
Cho đường tròn (O;R) đường kính AB.M trên đường tròn (O). điểm D trên đoạn thẳng AM.BD cắt đường tròn (O) tại K( khác B).AK cắt BM tại C. CD cắt AB tại Q VẼ HÌNH THÔI ạ
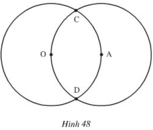
Trên hình 48, ta có hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C, D. Điểm A nằm trên đường tròn tâm O.
a) Vẽ đường tròn tâm C, bán kính 2cm.
b) Vì sao đường tròn (C; 2cm) đi qua O, A?
a) Vẽ đường tròn (C; 2cm)
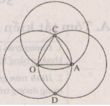
b)
Vì hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C nên:
- C thuộc (O; 2cm) ⇒ OC = 2cm do đó O thuộc (C; 2cm)
- C thuộc (A; 2cm) ⇒ AC = 2cm do đó A thuộc (C; 2cm)
Vậy đường tròn (C; 2cm) đi qua hai điểm O và A.
Đúng 0
Bình luận (0)