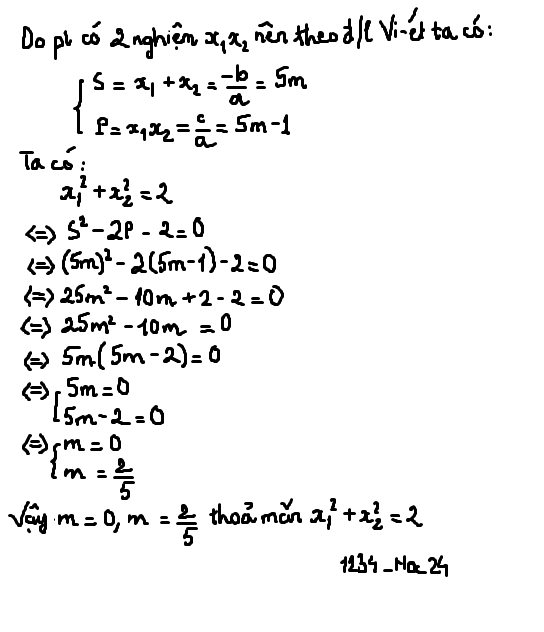cho phương trình bậc hai (ẩn x):
tìm m để phương trình luôn có 2 nghiệm phân biệt thỏa mãn

Những câu hỏi liên quan
cho phương trình bậc hai (ẩn x): \(x^2-4x+2(m-1)=0
\)
tìm m để phương trình luôn có 2 nghiệm phân biệt thỏa mãn \(x_1 + x_2 =2x_1x_2\)
Δ=(-4)^2-4(2m-2)
=16-8m+8=-8m+24
Để phương trình có hai nghiệm phân biệt thì -8m+24>0
=>m<3
x1+x2=2x1x2
=>2(2m-2)=4
=>2m-2=2
=>2m=4
=>m=2(nhận)
Đúng 0
Bình luận (0)
Cho phương trình x2- 2( m+1 )x+m2+4=0
Tìm các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x12 +2(m+1)x2 ≤ 2m2 + 20
x1+x2=2m+2; x1x2=m^2+4
x1^2+2(m+1)x2<=2m^2+20
=>x1^2+x2(x1+x2)<=2m^2+20
=>x1^2+x2x1+x2^2<=2m^2+20
=>(x1+x2)^2-x1x2<=2m^2+20
=>(2m+2)^2-(m^2+4)<=2m^2+20
=>4m^2+8m+4-m^2-4-2m^2-20<=0
=>m^2-8m-20<=0
=>m<=-10 hoặc m>2
Đúng 0
Bình luận (0)
\(x^2-2\left(m+1\right)x+m^2+4=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta'>0\) hay \(\Delta'=\left(m+1\right)^2-m^2-4=m^2+2m+1-m^2-4=2m-4>0\Leftrightarrow m>2\)
Theo hệ thức Viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+4\end{matrix}\right.\)
Vì \(x_1^2\) là nghiệm của phương trình (1) nên ta có : \(x_1^2-2\left(m+1\right)x+m^2+4=0\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta lại có : \(x_1^2+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-m^2-4\le2m^2+20\)
\(\Leftrightarrow4\left(m+1\right)^2-m^2\le2m^2+20\)
\(\Leftrightarrow4\left(m^2+2m+1\right)-m^2\le2m^2+20\)
\(\Leftrightarrow m^2+8m-16\le0\)
\(\Leftrightarrow-10\le m\le2\)
Kết hợp điều kiện....
Đúng 1
Bình luận (0)
cho phương trình ẩn x : x^2 +2(m+3)x. 2m-11 (1)
a/ chứng tỏ phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của m
b/ Tìm giá trị của m để phương trình (1) có hai nghiệm x1 ,x2 thỏa mãn hệ thức 1/x1+1/x2=2
Cho phương trình x2 + 2 ( m + 3 )x + 2m - 11
a) Ta có:
△' = b'2 - ac = ( m + 3 )2 - 1 . ( 2m - 11 )
m2 - 6m + 9 - 2m + 11
△' = b'2 - ac =
Đúng 0
Bình luận (0)
Cho,phương,trình:x^2-4x+m-1=0
Tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn điều kiện x1^2+x2^2=30
Áp dụng hệ thức vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=m-1\end{matrix}\right.\)
Ta có:
\(x_1^2+x^2_2=30\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=30\)
\(\Leftrightarrow4^2-2\left(m-1\right)=30\)
\(\Leftrightarrow2m-2=-14\)
\(\Leftrightarrow m=-6\)
Đúng 2
Bình luận (0)
Cho phương trình: x²-4x-m²+3=0
Tìm m để phương trình có hai nghiệm x1;x2 thỏa mãn: 5x1+x2
5x1+x2 thỏa mãn gì bạn nhỉ? Bạn bổ sung thêm đề nhé
Đúng 0
Bình luận (1)
Cho phương trình bậc hai ( ẩn x) : x² + 4x + m +1= 0 (*) (m là tham số)
a) Giải phương trình khi m = -1
b) Tìm m để phương trình có một nghiệm bằng 2.Tìm nghiệm còn lại.
c) Tìm m để phương trình có hai nghiệm x1,x2 thỏa mãn x12 + x12 =10.
a)thay m=1 vào pt ta có
\(x^2+4x=0\)
<=> \(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b) thay x=2 vào pt ta có: 13+m=0
<=>m=-13
thay m=-13 vào pt ta có
\(x^2+4x-12=0\)
<=>(x-2)(x+6)=0
<=>\(\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)\(\)
vậy với m=-13 thì nghiệm còn lại là x=-6
c) để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>16-4m-4>0
<=>3-m>0
<=>m<3
áp dụng định lí Vi-ét ta có\(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=m+1\end{matrix}\right.\)
theo đề bài ta có \(x_1^2+x_2^2=10\)
<=>\(\left(x_1+x_2\right)^2-2x_1x_2=10\)
<=>16-2m-2=10
<=>2-m=0
<=>m=2(nhận)
vậy với m=2 thì pt có 2 nghiệm pb thỏa yêu cầu đề bài.
Đúng 1
Bình luận (0)
Cho phương trình: x²-4x-m²+3=0
Tìm m để phương trình có hai nghiệm x1;x2 thỏa mãn: 5x1+x2=0
a=1; b=-4; c=-m^2+3
Δ=(-4)^2-4*1*(-m^2+3)
=16+4m^2-12=4m^2+4>=4>0
=>Phương trình luôn có hai nghiệm phân biệt
5x1+x2=0 và x1+x2=4
=>4x1=-4 và x1+x2=4
=>x1=-1 và x2=5
x1x2=-m^2+3
=>-m^2+3=-5
=>m^2-3=5
=>m^2=8
=>\(m=\pm2\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho phương trình : x2 - 5mx + 5m - 1 = 0
Tìm m để phương trình có 2 nghiệm phân biệt x1, x2
Thỏa mãn: x12 + x2 2 = 2
Cho phương trình : x2 - 5mx + 5m - 1 = 0
Tìm m để phương trình có 2 nghiệm phân biệt x1, x2
Thỏa mãn: x12 + x2 2 = 2
\(\text{∆}=\left(-5m\right)^2-4.\left(5m-1\right)\)
\(=25m^2-20m+4\)
\(=\left(5m-2\right)^2>0\forall m\)
Đúng 3
Bình luận (0)
Do phương trình có 2 nghiệm x1, x2
\(\Rightarrow\left\{{}\begin{matrix}S=x_1+x_2=5m\\P=x_1.x_2=5m-1\end{matrix}\right.\)
Ta có:
\(x_1^2+x_2^2=2\)
\(\left(x_1^2+2x_1x_2+x_2^2\right)-2x_1x_2=2\)
\(\left(x_1+x_2\right)^2-2x_1x_2-2=0\)
\(\left(5m^2\right)-2\left(5m-1\right)-2=0\)
\(25m^2-10m+2-2=0\)
\(25m^2-10m=0\)
\(5m\left(5m-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{2}{5}\end{matrix}\right.\)
Vậy ...
Đúng 5
Bình luận (0)