GIÚP MÌNH VS Xác định toạ độ giao điểm của đồ thị 2 hàm số (P):y=x^2/2 và (d): y= -x+3/2

Những câu hỏi liên quan
Trong cùng một hệ toạ độ , gọi (P ) là đồ thị của hàm số y = x2 và (d) là đồ thị
của hàm số y = -x + 2 xác định toạ độ giao điểm của (P) và (d)
Xét pt hoành độ gđ của (P) và (d):
\(x^2=-x+2\)
\(\Leftrightarrow x^2+x-2=0\) \(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Thay x=-2 vào (P) ta đc: y=4
Thay x=1 vào (P) ta đc: y=1
Vậy hoành độ gđ của (P) và (d) là (-2;4) và (1;1)
Đúng 2
Bình luận (0)
Cho hàm số y=2/3 x2 có đồ thị P và y= x + 5/3 có đồ thị D a. Vẽ P và D trên cùng một hệ trục toạ độ vuông góc b. Xác định toạ độ các giao điểm của P và D c. Gọi A là điểm thuộcP và B là điểm thuộc D sao cho { x A = x B 11 y A = 8 y B xác định toạ độ của A và B
câu 1: a) vẽ parabol (p): y 1/2x^2 và đường thẳng (d): y3/2x-1 trên cùng 1 mặt phẳng toạ độb) xác định toạ độ giao điểm của (p) và (d) bằng phép toáncâu 2: a) vẽ đồ thị hàm số (p): yx^2 và (d): Y-x+2 trên cùng 1 hệ trục toạ độb) xác định toạ độ giao điểm của (p) và (d)câu 3: cho hai hàm số yx^2 và y-2x+3a) vẽ các đồ thị của hai hàm số này trên cùng một hệ trục toạ độb) tìm toạ độ giao điểm của hai đồ thị đó
Đọc tiếp
câu 1: a) vẽ parabol (p): y= 1/2x^2 và đường thẳng (d): y=3/2x-1 trên cùng 1 mặt phẳng toạ độ
b) xác định toạ độ giao điểm của (p) và (d) bằng phép toán
câu 2: a) vẽ đồ thị hàm số (p): y=x^2 và (d): Y=-x+2 trên cùng 1 hệ trục toạ độ
b) xác định toạ độ giao điểm của (p) và (d)
câu 3: cho hai hàm số y=x^2 và y=-2x+3
a) vẽ các đồ thị của hai hàm số này trên cùng một hệ trục toạ độ
b) tìm toạ độ giao điểm của hai đồ thị đó
Cho đồ thị hàm số y=3x+2 d a, vẽ b, xác định toạ độ giao điểm d và (d1) y= -x +6
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x+2=-x+6\\y=-x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Gọi (d1) là đồ thị hàm số y = m x + 2 và
(d2) là đô thị hàm số y = 1 x – 1 2
a) Với m = - 12 , xác định toạ độ giao điểm của (d1) và (d2)
b) Xác định giá trị của m để M(- 3; - 3) là giao điểm của (d1) , (d2)
a) Vẽ trên cùng một mặt phẳng toạ độ Oxy đồ thị các hàm số sau (d_{i}) / y = - 1/2 * x - 2(d_{2}) / y = 1/4 * x + 2 b) Gọi giao điểm của hai đường thăng (d) và (d2) với trục tung lần lượt là M và N ; giao điểm của (d)và (d) là P. Xác định toạ độ của M, N và P
a) 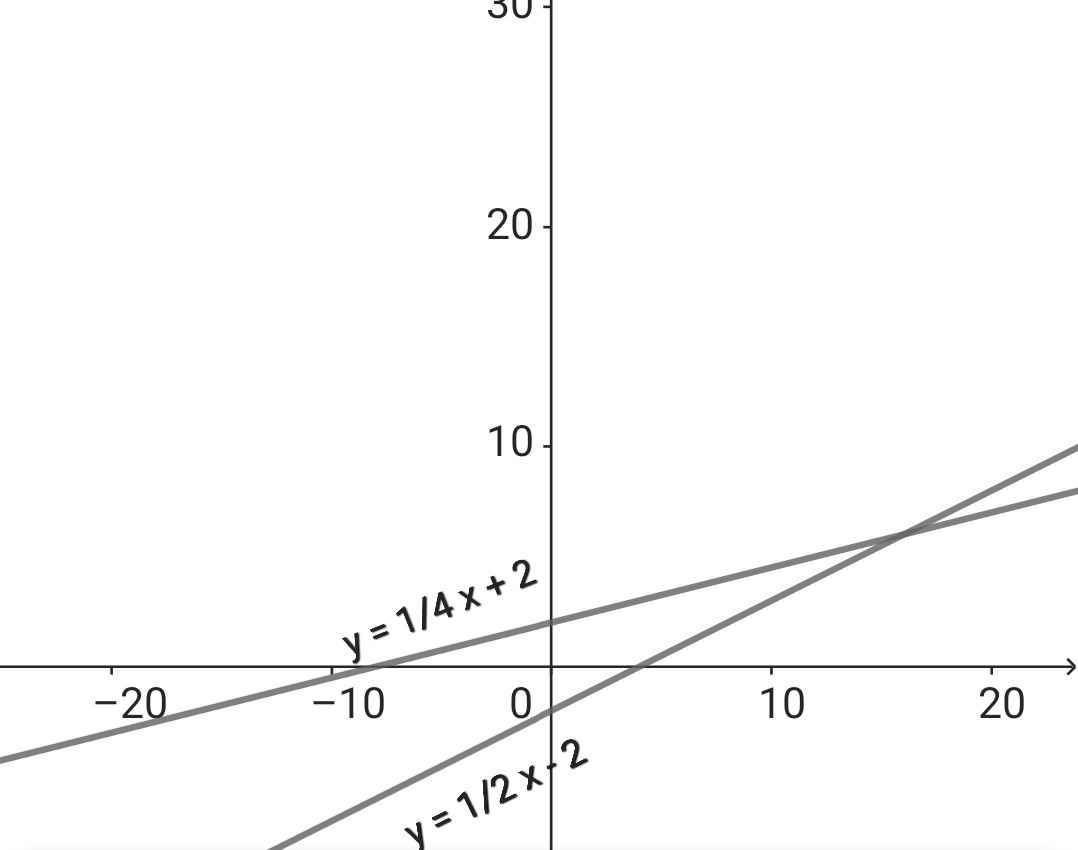
b) *) Thay x = 0 vào (d) ta có:
y = 1/2 . 0 - 2 = -2
⇒ M(0; -2)
Thay x = 0 vào (d) ta có:
y = 1/4 . 0 + 2 = 2
⇒ N(0; 2)
Phương trình hoành độ giao điểm của (d) và (d)
1/2 x - 2 = 1/4 x + 2
⇔ 1/2 x - 1/4 x = 2 + 2
⇔ 1/4 x = 4
⇔ x = 4 : (1/4)
⇔ x = 16
Thay x = 16 vào (d) ta có:
y = 1/2 . 16 - 2 = 6
⇒ P(16; 6)
Đúng 2
Bình luận (0)
Câu 3: Cho các hàm số \(y=2x+5\) và \(y=-x+2\)
a. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng toạ độ Oxy.
b. Dựa vào hình vẽ, xác định toạ độ giao điểm A của hai đồ thị hàm số.
c. Hai đồ thị của hai hàm số đã cho cắt trục hoành tại các điểm B và C. Tính diện tích tam giác ABC
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
Đúng 1
Bình luận (0)
xác định toạ độ giao điểm của 2 đồ thị hàm số y=2x và y= -x+1 mà không phải vẽ đồ thị.
Hoành độ của giao điiểm là :
2x = -x + 1
2x + x = 1
3x = 1
x = 1/3
Thay x = 1/3 ta có :
y = 2.x=2.1/3 = 2/3
VẬy giao điểm là : ( 1/3 ; 2/3)
Đúng 0
Bình luận (0)
Cho parabol(P):y= x^2 và đường thẳng(d):y=x+2
a)Vẽ đồ thị 2 hàm số trên,trên cùng 1 hệ trục toạ độ
b) Xác định toạ độ giao điểm A,B của 2 đồ thị trên
c) Cho điểm M thuộc Parabol(P) có hoành độ là m nhỏ thoả mãn
-1 ≤m ≤2. Chứng minh Diện tích MAB ≤ 27/8
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)
Đúng 0
Bình luận (0)


















