cho tam giác ABC có 3 đường cao AB=BE=CF . Chứng minh rằng khi đó tam giác ABC là tam giác đều
Những câu hỏi liên quan
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Tham khảo:
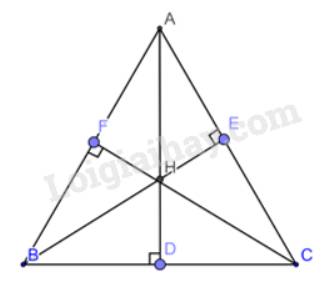
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC , các đường cao BE và CF a, chứng minh tam giác AEB đồng dạng với tam giác AFC. Từ đó suy ra AF. AB=AE.AC b, chứng minh góc AEF=ABC c, nếu tam giác ABC có có góc A=60°. Chứng minh rằng SABC=4SAEF
a) cho ABC ,vẽ đường thẳng đi qua A cắt BC tại K và cắt trung tuyến BM tại I sao cho BI:IM= 1:2 Tính ti số diện tích của tam giác ABK và điện tích tam giác ABC b) Cho tam giác ABC có 3 đường cao AD,BE,CF thỏa mãn AD+BC=BE+AC=CF+AB Chứng minh tam giác ABC là tam giác đều
cho tam giác abc, 3 đường cao AD, BE,CF. Biết AD=BE=CF. chứng minh tam giác ABC đều
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H. 1) Chứng minh rằng: AE.AC AF.AB2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC4) Chứng minh rằngBF.BA+CE.CA BC2
Đọc tiếp
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
1) Chứng minh rằng: AE.AC = AF.AB
2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB
3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC
4) Chứng minh rằngBF.BA+CE.CA = BC2
1: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
2: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng vơi ΔABC
3: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF/HB=HE/HC
Xét ΔHFE và ΔHBC có
HF/HB=HE/HC
góc FHE=góc BHC
=>ΔFHE đồng dạng với ΔBHC
Đúng 1
Bình luận (0)
cho tam giác ABC có góc A = 60 độ. Gọi BE và CF là hai đường cao và M trung điểm của BC. Chứng minh rằng tam giác MFE là tam giác đều.
Cho tam giác nhọn ABC có 3 đường cao AB, BE, CF. Biết AD=BE=CF
Chứng minh rằng ΔABC đều
Xét ΔAFC vuông tại F và ΔAEB vuông tại E có
CF=BE
góc ACF=gócABE
=>ΔAFC=ΔAEB
=>AC=AB
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
EB=DA
góc C chung
=>ΔCEB=ΔCDA
=>CB=CA=AB
=>ΔABC đều
Đúng 1
Bình luận (0)
Giả sử AD, BE và CF là các đường phân giác trong của tam giác ABC. Chứng minh rằng tam giác ABC đều khi và chỉ khi diện tích tam giác DEF bằng 1/ 4 diện tích tam giác ABC.
có cần rườm rà thế ko bn? mk chỉnh đề nhé
cho ΔABC cân tại A. trung truyến BM,CN cắt nhau tại I. CMR AI là p/g ∠BAC
vì BM và CN là 2 trung truyến của 1 Δ và cắt nhau tại I
=> I là trọng tâm ΔABC => AI là trung tuyến mà ΔABC cân tại A nên AI là p/g ∠BAC
Đúng 0
Bình luận (0)
a) Cho tam giác ABC, vẽ đường thẳng đi qua A cắt cạnh BC tại K và cắt trung tuyến BM tại I sao cho BI : IM = 1:2 Tính tỉ số diện tích của tam giác ABK và diện tích tam giác ABC
b) Cho tam giác ABC có ba đường cao AD, BE và CF thỏa mãn AD + BC = BE + AC = CF + AB
Chứng minh tam giác ABC là tam giác đều