Giải các hệ pt và tìm nghiệm:
a) 6x2 - 75x - 81 = 0
b) 5x2 - 32x + 27 = 0
Giải pt bằng delta và tìm nghiệm:
a) 2x2 - 5x + 1 = 0
b) 4x2 + 4x + 1 =0
c) 5x2 - x + 2 =0
a) \(2x^2-5x+1=0\)
\(\Delta=b^2-4ac\Rightarrow\left(-5\right)^2-4.2.1=17>0\)
Phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)+\sqrt{17}}{2.2}=\dfrac{5+\sqrt{17}}{4}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)-\sqrt{17}}{2.2}=\dfrac{5-\sqrt{17}}{4}\)
___________________________________________________
b) \(4x^2+4x+1=0\)
\(\Delta=b^2-4ac\Rightarrow4^2-4.4.1=0\)
Vậy phương trình có nghiệm kép:
___________________________________________________
c) \(5x^2-x+2=0\)
\(\Delta=b^2-4a\Rightarrow\left(-1\right)^2-4.5.2=-39\)
Vậy phương trình vô nghiệm.
\(a,2x^2-5x+1=0\)
\(\Delta=-b^2-4ac\)
\(\Delta=25-8\)
\(\Delta=17\)
Vậy phương trình có `2` nghiệm phân biệt :
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{17}}{4} \)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{17}}{4}\)
\(b,4x^2+4x+1=0\)
\(\Delta=b^2-4ac\)
\(\Delta=16-16=0\)
Vậy phương trình có nghiệm kép :
\(x=\dfrac{-b}{2a}=-\dfrac{4}{8}=-\dfrac{1}{2}\)
\(c,5x^2-x+2=0\)
\(\Delta=1-40\)
\(\Delta=-39\)
Vậy phương trình vô nghiệm .
cứu ạ
Bài 1: Giải các pt và hệ pt sau:
a) 3xmũ2 – 7x + 2 = 0
b) xmũ 4 – 5x + 4 = 0
a: =>3x^2-6x-x+2=0
=>(x-2)(3x-1)=0
=>x=2 hoặc x=1/3
b: =>x^4-x-4x+4=0
=>x(x-1)(x^2+x+1)-4(x-1)=0
=>(x-1)(x^3+x^2+x-4)=0
=>x-1=0 hoặc x^3+x^2+x-4=0
=>x=1 hoặc x=1,15
a)giải PT x3-6x2-x+30=0
b)tìm giá trị nhỏ nhất của bt x2-12x+33
a: =>x^3+2x^2-8x^2-16x+15x+30=0
=>(x+2)(x^2-8x+15)=0
=>(x+2)(x-3)(x-5)=0
=>\(x\in\left\{-2;3;5\right\}\)
b: =x^2-12x+36-3
=(x-6)^2-3>=-3
Dấu = xảy ra khi x=6
Phương trình nào sau đây vô nghiệm:
A, x-1=0
B, 5x2+10=0
C, x2-3=6
D, x2+6=-9
Vì sao phương trình đó vô nghiệm
Chọn B và D
Phương trình B vô nghiệm vì \(5x^2+10\ge10>0\forall x\)
Phương trình C vô nghiệm vì \(x^2+6\ge6>-9\forall x\)
B và C
vì \(5x^2+10=0\Leftrightarrow5x^2=-10\Leftrightarrow x^2=-2\)(VL)
\(x^2+6=-9\Leftrightarrow x^2=-15\left(VL\right)\)
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn). 1) x2 - 11x + 38 = 0 ; 2) 6x2 + 71x + 175 = 0 ; 3) 5x2 - 6x + 27 = 0 ; 4) - 30x2 + 30x - 7,5 = 0 ; 5) 4x2 - 16x + 17 = 0 ; 6) x2 + 4x - 12 = 0 ;
1, \(\Delta=\left(-11\right)^2-4.1.38=121-152=-31< 0\)
\(\Rightarrow\) pt vô nghiệm
2, \(\Delta=71^2-4.6.175=5041-4200=841\)
\(x_1=\dfrac{-71+\sqrt{841}}{2.6}=\dfrac{-71+29}{12}=\dfrac{-42}{12}=-\dfrac{7}{2}\)
\(x_2=\dfrac{-71-\sqrt{841}}{2.6}=\dfrac{-71-29}{12}=\dfrac{-10}{12}=-\dfrac{25}{3}\)
3, \(\Delta=\left(-3\right)^2-5.27=9-135=-126< 0\)
⇒ pt vô nghiệm
4, \(\Delta=15^2-\left(-30\right)\left(-7,5\right)=225-225=0\)
\(\Rightarrow x_1=x_2=\dfrac{-30}{2.\left(-30\right)}=\dfrac{1}{2}\)
5, \(\Delta'=\left(-8\right)^2-4.17=64-68=-4\)
⇒ pt vô nghiệm
6, \(\Delta=4^2-4.1.\left(-12\right)=16+48=64\)
\(x_1=\dfrac{-4+\sqrt{64}}{2.1}=\dfrac{-4+8}{2}=\dfrac{4}{2}=2\)
\(x_2=\dfrac{-4-\sqrt{64}}{2.1}=\dfrac{-4-8}{2}=\dfrac{-12}{2}=-6\)
Giải các phương trình và hệ phương trình sau:
a , 5 x 2 − 16 x + 3 = 0 b , x 4 + 9 x 2 − 10 = 0 c , 3 x − 2 y = 10 x + 3 y = 7
a) Ta có: Δ = 196 > 0
Phương trình có 2 nghiệm x 1 = 3 , x 2 = 1 5
b) Đặt t = x 2 , t ≥ 0 , phương trình trở thành t 2 + 9 t − 10 = 0
Giải ra được t=1 (nhận); t= -10 (loại)
Khi t=1, ta có x 2 = 1 ⇔ x = ± 1 .
c) 3 x − 2 y = 10 x + 3 y = 7 ⇔ 3 x − 2 y = 10 ( 1 ) 3 x + 9 y = 21 ( 2 )
(1) – (2) từng vế ta được: y=1
Thay y= 1 vào (1) ta được x= 4
Vậy hệ phương trình có nghiệm duy nhất là x= 4; y= 1.
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7 x 2 − 2 x + 3 = 0 b ) 5 x 2 + 2 10 x + 2 = 0 c ) 1 2 x 2 + 7 x + 2 3 = 0 d ) 1 , 7 x 2 − 1 , 2 x − 2 , 1 = 0
a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai 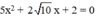
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai 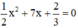
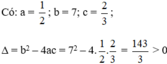
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 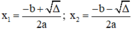
+ Nếu Δ = 0, phương trình có nghiệm kép 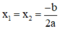 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.
Tìm x:
a) 64x5-4x3=0
b) x3-81x=0
c) x(5-3x)-5+3x=0
d) 4x3+12x2-9x-27=0
e) x4-6x2+7=0
Tìm x:
a) 64x5-4x3=0
b) x3-81x=0
c) x(5-3x)-5+3x=0
d) 4x3+12x2-9x-27=0
e) x4-6x2+7=0