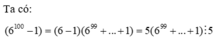Chứng minh rằng 6100 - 1 chia hết cho 5

Những câu hỏi liên quan
Bài 2:
1.Chứng minh rằng : 9999931999 - 555551997 chia hết cho 5
2.Chứng minh rằng : 1725 - 1321 + 244 Chia hết cho 10
3. Chứng minh rằng: 172008 - 112008 - 32008 + 1 chia hết cho 10
a) Ta thấy \(999993^{1999}⋮̸5\) và \(55555^{1997}⋮5\) nên \(999993^{1999}-55555^{1997}⋮̸5\), mâu thuẫn đề bài.
b)
Ta có \(17^{25}=17^{4.6+1}=17.\left(17^4\right)^6=17.\overline{A1}=\overline{B7}\) có chữ số tận cùng là 7. \(13^{21}=13^{4.5+1}=13.\left(13^4\right)^5=13.\overline{C1}=\overline{D3}\) có chữ số tận cùng là 3. \(24^4=4^4.6^4=\overline{E6}.\overline{F6}=\overline{G6}\) có chữ số tận cùng là 6 nên \(17^{25}-13^{21}+24^4\) có chữ số tận cùng là chữ số tận cùng của \(7-3+6=10\) hay là 0. Vậy \(17^{25}-13^{21}+24^4⋮10\)
c) Cách làm tương tự câu b.
Đúng 2
Bình luận (0)
Chứng minh ( 6 100 − 1 ) ⋮ 5
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: ( 6 100 − 1 ) = ( 6 − 1 ) ( 6 99 + ... + 1 ) = 5 ( 6 99 + ... + 1 ) ⋮ 5 |
Đúng 0
Bình luận (0)
Chứng minh ( 6 100 - 1 ) ⋮ 5
b1.Cho AB = 2CD .Chứng minh rằng ABCD chia hết cho 67
b2.chứng minh N.(n+1).(2n+1) chia hết cho 2 và 3
b3. chứng minh rằng
a.4n - 5 chia hết cho 2n - 1
b.2.(2n - 1) -3 chia hết cho 2n -1
Bài 3:
a: =>4n-2-3 chia hết cho 2n-1
=>\(2n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{1;0;2;-1\right\}\)
b: =>-3 chia hết cho 2n-1
=>\(2n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{1;0;2;-1\right\}\)
Đúng 0
Bình luận (0)
a) Cho các số tự nhiên x ; y. Biết 3x + 2y + 11 chia hết cho 15. Hỏi 18x + 2y + 26 có chia hết cho 15 không? Vì sao?
b) Chứng tỏ rằng 6100 - 1 chia hết cho 5
c) Khi chia một số cho 273 ta được số dư là 182. Hỏi số đó có chia hết cho 91 không? Vì sao?
d) 3 + 32 + 33 + 34 + 35+ 36 + 37 + .... + 360 chia hết cho 4
Câu d là 3 + 32 + 33 + 34 + 35+ 36 + 37 + .... + 360 chia hết cho 4 nhé! Viết vội quá nên quên ![]() , sorry
, sorry
d) (3+32)+(33+34)+(35+36)+...+(359+360)
= 3.(1+3)+33.(1+3)+35.(1+3)+...+359(1+3)
= 3.4+33.4+35.4+...+359.4
= 4.(3+33+35+...+359) chia hết cho 4
Vậy 3+32+33+34+35+36+37+...+360 chia hết cho 4
Đúng 0
Bình luận (0)
b) Ta có: 6100-1
= 699.6-1
= 699.(6-1)
= 699.5
Vì 699. 5 chia hết cho 5 nên 6100-1 chia hết cho 5
Vậy 6100-1 chia hết cho 5
Đúng 1
Bình luận (0)
1. a, Cho B 3 + 3^3 + 3^5 +...+ 3^1991. Chứng minh rằng: B chia hết cho 3 ; B chia hết cho 41b, Chứng minh rằng: (99^5 - 98^4 - 97^3 - 96^3) chia hết cho 2, cho 5.c, A 999993^1999 - 555557^1997. Chứng minh: A chia hết cho 5. d, A 8n + 111..1 ( n chữ số 1 ). Chứng minh: A chia hết cho 9.e, Cho ( abc + deg ) chia hết cho 37. Chứng minh: abcd chia hết chio 37.2. Tìm 2 số biết rằng tổng của chúng gấp 7 lần hiệu của chúng, còn tích của chúng gấp 192 lần hiệu của chúng.3. Tìm s...
Đọc tiếp
1. a, Cho B = 3 + 3^3 + 3^5 +...+ 3^1991. Chứng minh rằng: B chia hết cho 3 ; B chia hết cho 41
b, Chứng minh rằng: (99^5 - 98^4 - 97^3 - 96^3) chia hết cho 2, cho 5.
c, A = 999993^1999 - 555557^1997. Chứng minh: A chia hết cho 5.
d, A = 8n + 111..1 ( n chữ số 1 ). Chứng minh: A chia hết cho 9.
e, Cho ( abc + deg ) chia hết cho 37. Chứng minh: abcd chia hết chio 37.
2. Tìm 2 số biết rằng tổng của chúng gấp 7 lần hiệu của chúng, còn tích của chúng gấp 192 lần hiệu của chúng.
3. Tìm số nhỏ hơn 100, biết rằng khi chia số đó cho 5 thì được dư là 3, chia cho 11 dư 5.
1)
a)\(B=3+3^3+3^5+3^7+.....+3^{1991}\)
\(\Leftrightarrow B=3\left(1+3^2+3^4+3^6+.....+3^{1990}\right)\)
Vì \(3\left(1+3^2+3^4+3^6+.....+3^{1990}\right)\)chia hết cho 3 nên \(B⋮3\)
\(B=3+3^3+3^5+3^7+.....+3^{1991}\)
\(\Leftrightarrow B=\left(3+3^3+3^5+3^7\right)+.....+\left(3^{1988}+3^{1989}+3^{1990}+3^{1991}\right)\)
\(\Leftrightarrow B=3\left(1+3^2+3^4+3^6\right)+.....+3^{1988}\left(1+3^2+3^4+3^6\right)\)
\(\Leftrightarrow B=3.820+.....+3^{1988}.820\)
\(\Leftrightarrow B=3.20.41+.....+3^{1988}.20.41\)
Vì \(3.20.41+.....+3^{1988}.20.41\) chia hết cho 41 nên \(B⋮41\)
Đúng 0
Bình luận (0)
1. Cho A = \(2^{2016}-1\) . Chứng minh rằng A chia hết cho 105.
2.Chứng minh rằng \(5^{2017}+7^{2015}\) chia hết cho 12.
3. Chứng minh rằng B = \(3^{2^{2n}}+10\) chia hết cho 13.
4. Chứng minh rằng C = \(3^{2^{4n+1}}+2^{3^{4n+1}}+5\) luôn chia hết cho 22.
1. \(A=2^{2016}-1\)
\(2\equiv-1\left(mod3\right)\\ \Rightarrow2^{2016}\equiv1\left(mod3\right)\\ \Rightarrow2^{2016}-1\equiv0\left(mod3\right)\\ \Rightarrow A⋮3\)
\(2^{2016}=\left(2^4\right)^{504}=16^{504}\)
16 chia 5 dư 1 nên 16^504 chia 5 dư 1
=> 16^504-1 chia hết cho 5
hay A chia hết cho 5
\(2^{2016}-1=\left(2^3\right)^{672}-1=8^{672}-1⋮7\)
lý luận TT trg hợp A chia hết cho 5
(3;5;7)=1 = > A chia hết cho 105
2;3;4 TT ạ !!
Đúng 0
Bình luận (0)
Cho A=1+5+5^2+5^3+5^4+5^5+...................+5^99
a,Chứng minh rằng A chia hết cho 6
b,Chứng minh rằng A chia hết cho 156
Bạn tham khảo ở đây: Câu hỏi của Mật khẩu trên 6 kí tự - Toán lớp 6 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
1) Chứng minh rằng nếu a chia hết cho m và b chia hết cho n thi a.b chia hết cho m.n
2)Chứng minh rằng nếu n chia hết cho 12(n khac 0) thì 1+3+5+7+.....+(2n-1) chia hết cho 144
Bài 1: Chứng minh rằng
a) P = (a+5)(a+8) chia hết cho 2
b) Q = ab(a+b) chia hết cho 2
Bài 2: cho a thuộc N. chứng minh a2-8 không chia hết cho 5
Bài 3: Chứng minh rằng n5-n chia hết cho 10
Bài 1:
a) P=(a+5)(a+8) chia hết cho 2
Nếu a chẵn => a+8 chẵn=> a+8 chia hết cho 2 => (a+5)(a+8) chia hết cho 2
Nếu a lẽ => a+5 chẵn => a+5 chia hết cho 2 => (a+5)(a+8) chia hết cho 2
Vậy P luôn chia hết cho 2 với mọi a
b) Q= ab(a+b) chia hết cho 2
Nếu a chẵn => ab(a+b) chia hết cho 2
Nếu b chẵn => ab(a+b) chia hết cho 2
Nếu a và b đều lẽ => a+b chẵn => ab(a+b) chia hết cho 2
Vậy Q luôn chia hết cho 2 với mọi a và b
Đúng 0
Bình luận (0)
bài 3:n5- n= n(n-1)(n+1)(n2+1)=n(n-1)(n+1)(n2+5-4)=n(n-1)(n+1)(n-2)(n+2)+5n(n-1)(n+1).
Vì: n(n-1)(n+1)(n-2)(n+2) là 5 số nguyên liên tiếp thì chia hết cho 10 (1)
ta lại có: n(n+1) là 2 số nguyên liên tiếp nên chia hết cho 2
=> 5n(n-1)n(n+1) chia hết cho 10 (2)
Từ (1) và (2) => n5- n chia hết cho 10
Đúng 0
Bình luận (0)
a) a lẻ suy ra a+5 chia hết cho 2
a chẵn suy ra a+8 chia hết cho 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời