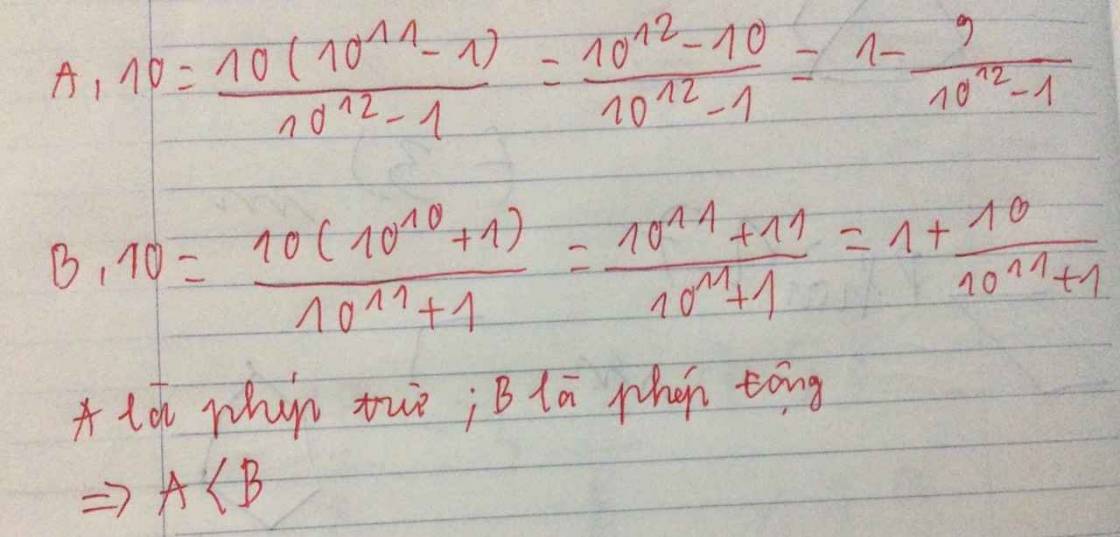a. 19/10 > 10/11

b. 11/10 = 12/11

c. 9/10 = 10/11

a)\(\dfrac{19}{10}>\dfrac{10}{11}\)

b)\(\dfrac{11}{10}=\dfrac{12}{11}\)

c)\(\dfrac{9}{10}< \dfrac{10}{11}\)

10/11 < 11/12

10/ 11 và 11/12

Ta có :1-10/11=1/11

          1-11/12=1/12

Vì 1/11 > 1/12.Nên 10/11 < 11/12

11/12 lớn hơn

ĐỀ : \(A=\frac{10^{11}-1}{10^{12}-1}\)và \(B=\frac{10^{10}+1}{10^{11}+1}\).

Ta có : \(10A=\frac{10\left(10^{11}-1\right)}{10^{12}-1}=\frac{10^{12}-10}{10^{12}-1}=\frac{10^{12}-1-9}{10^{12}-1}\)\(=1-\frac{9}{10^{12}-1}\).

            \(10B=\frac{10\left(10^{10}+1\right)}{10^{11}+1}=\frac{10^{11}+10}{10^{11}+1}=\frac{10^{11}+1+9}{10^{11}+1}\)\(=1+\frac{9}{10^{11}+1}\).

Ta so sánh : \(1-\frac{9}{10^{12}-1}< 1+\frac{9}{10^{11}+1}\)hay \(10A< 10B.\)

\(\Rightarrow A< B\left(đpcm\right)\)

\(A=\dfrac{10^{11}+1}{10^{12}-1}\)

\(\Rightarrow10A=\dfrac{10^{11}+1}{10^{12}-1}.10\)

\(\Rightarrow10A=\dfrac{10\left(10^{11}+1\right)}{10^{12}-1}\)

\(\Rightarrow10A=\dfrac{10^{12}-10}{10^{12}-1}\)

\(B=\dfrac{10^{10}+1}{10^{11}+1}\)

\(\Rightarrow10B=\dfrac{10^{10}+1}{10^{11}+1}.10\)

\(\Rightarrow10B=\dfrac{\left(10^{10}+1\right).10}{10^{11}+1}\)

\(\Rightarrow10B=\dfrac{10^{11}+10}{10^{11}+1}\)

Ta thấy:

 \(10^{12}-1>10^{12}-10>0\Rightarrow10A< 1\)

\(0< 10^{11}+1< 10^{11}+10\Rightarrow10B>1\)

Mà \(10A< 1;10B>1\)

\(\Rightarrow B>A\).

Bạn tham khảo cách giải này ạ: 

Nếu có 1  phân số \(\dfrac{a}{b}\) < 1 thì a/b < a+n/b+n.

Tương tự ta có: A <   (1011 -1)+11/(1012-1)+10

                        A < 1011+10/1012+10

                        A < 10(1010+1)/10(1011+1)

                        A < 10(1010+1)/10(1011+1)

                        A < 1010+1/1011+1

Vậy A< B ( đcpcm )

mình nghĩ là b

 B/A= [(10^10 + 1)/(10^11 + 1)]/[(10^11 - 1)/(10^12 - 1)] 
= [(10^12 - 1).(10^10 + 1)]/[(10^11 - 1).(10^11 + 1)] 
= [(10^22 - 1) + (10^12 - 10^10) ]/((10^22 - 1) 
= 1 + (10^12 - 10^10)/(10^22 - 1) > 1 
=> B > A

 A=10^11-1/10^12-1 < B=10^10+1/10^11=1.

B/A= [(10^10 + 1)/(10^11 + 1)]/[(10^11 - 1)/(10^12 - 1)] 
= [(10^12 - 1).(10^10 + 1)]/[(10^11 - 1).(10^11 + 1)] 
= [(10^22 - 1) + (10^12 - 10^10) ]/((10^22 - 1) 
= 1 + (10^12 - 10^10)/(10^22 - 1) > 1 
=> B > A

Lời giải:

$B=\frac{10^{11}+10}{10^{12}+10}$

Đặt $10^{11}-1=a; 10^{12}-1=b$ thì $0< a< b$. Khi đó:

$A-B=\frac{a}{b}-\frac{a+11}{b+11}=\frac{11(a-b)}{b(b+11)}<0$

$\Rightarrow A< B$

Dễ vãi

Hỏi 24.10.0.09.98.98888876676.978687877877.9866533145.6655543227.665433346.7646676:2

T

G