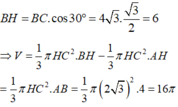cho tam giác ABC cân tại B có cạnh AB=4 và vecto AB.vectoBC= -8. Tính góc BAC

Những câu hỏi liên quan
Cho tam giác cân ABC cân tại A. Tia phân giác của góc BAC cắt cạnh BCtại M.1) Chứng minh tam giác AMB tam giác AMC.2) a- Biết góc BAC 500. Tính góc ABC và góc ACB.b- Biết BC 6 cm; AM 4 cm. Tính độ dài AB, AC?3) Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F. Chứng minh tam giác AEF cân.4) Kẻ EI vuông góc BC tại I. Gọi K là giao của đường thẳng EI và đường thẳng AC. Chứngminh A là trung điểm của đoạn KF.
Đọc tiếp
Cho tam giác cân ABC cân tại A. Tia phân giác của góc BAC cắt cạnh BC
tại M.
1) Chứng minh tam giác AMB = tam giác AMC.
2) a- Biết góc BAC = 500. Tính góc ABC và góc ACB.
b- Biết BC = 6 cm; AM = 4 cm. Tính độ dài AB, AC?
3) Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F. Chứng minh tam giác AEF cân.
4) Kẻ EI vuông góc BC tại I. Gọi K là giao của đường thẳng EI và đường thẳng AC. Chứng
minh A là trung điểm của đoạn KF.
1: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
2:
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)
b: BC=6cm nên BM=3cm
=>AB=AC=5cm
3: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
Đúng 2
Bình luận (1)
Tam giác ABC cân tại A. Điểm D thuộc cạnh AB sao cho tam giác ACD cân tại D và tam giác BCD cân tại C. Tính góc BAC
Cho tam giác ABC cân tại A có AB<BC.Trên cạnh BC lấy hai điểm M và N sao cho BM=CN=AB.
a)Chứng minh rằng tam giác AMN cân.
b)Tính các góc của tam giác AMN khi góc BAC=120 độ.
Xét tam gia ABM va ANC co:
AB = AC(gt)
\(\widehat{B}\) =\(\widehat{C}\) (gt)
BM =NC (gt)
=> \(\Delta\) ABM =\(\Delta\) ANC (C.G.C)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc
A
^
110
°
. Đường trung trực của các cạnh AB và AC cắt nhau tại I. Chứng minh:a) tam giác BIC cân;b)
B
I
C
^
2
(
180
°
-
B
A
C
^
)
và...
Đọc tiếp
Cho tam giác ABC có góc A ^ = 110 ° . Đường trung trực của các cạnh AB và AC cắt nhau tại I. Chứng minh:
a) tam giác BIC cân;
b) B I C ^ = 2 ( 180 ° - B A C ^ ) và tính số đo góc B I C ^ .
Cho tam giác ABC cân tại A, góc
B
A
C
^
120
°
và AB4cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC A.
16
3
π
B.
16
π
3
C.
16...
Đọc tiếp
Cho tam giác ABC cân tại A, góc B A C ^ = 120 ° và AB=4cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC
A. 16 3 π
B. 16 π 3
C. 16 π 3
D. 16 π
Chọn đáp án D
Phương pháp
Sử dụng công thức tính thể tích khối nón có chiều cao h và bán kính đáy r là
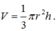
Cách giải
Áp dụng định lí cosin trong tam giác ABC ta có:
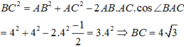
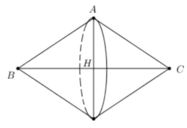
+) Gọi H là trung điểm của BC.
Khi quay tam giác ABC quanh cạnh BC ta được 2 hình nón có chung bán kính đáy AH, đường cao lần lượt là BH và CH với
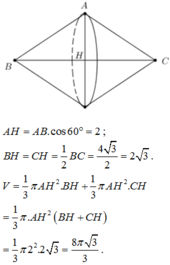
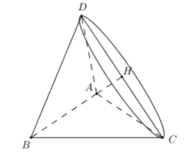
+) Khi quay tam giác ABC quanh AB ta được khối tròn xoay như sau:
Gọi D là điểm đối xứng C qua AB, H là trung điểm của CD
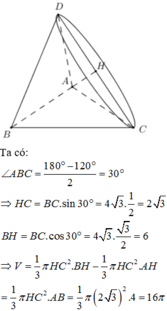
+) Do điểm B và C có vai trò như nhau nên khi quay tam giác ABC quanh AC ta cũng nhận được khối tròn xoay có thể tích bằng 16.
Vậy thể tích lớn nhất có thể được khi quay tam giác ABC quanh một đường thẳng chứa cạnh của tam giác ABC là 16π
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, góc
B
A
C
^
120
o
và AB 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
Đọc tiếp
Cho tam giác ABC cân tại A, góc B A C ^ = 120 o và AB = 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
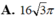
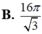
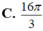
![]()
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Xem chi tiết
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Xem chi tiết
Sửa đề: Chứng minh \(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
\(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AM}\)
\(\overrightarrow{AC}-\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AC}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AC}-\overrightarrow{MC}\)
=>\(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
Đúng 0
Bình luận (0)
Cho tam giác abc có ab=6 ac=8 bc=10 đường phân giác của góc bac cắt cạnh bc tại d
a) tính db và dc
b) tính tỉ số diện tích của hai tam giác adb và adc
A) áp dụng tính chất đường phân giác
có : \(\dfrac{BD}{DC}\)=\(\dfrac{AB}{AC}\)=6/8=3/4
=>\(\dfrac{BD}{3}\)=\(\dfrac{DC}{4}\)=\(\dfrac{10}{7}\)
=>BD=3.10/7=30/7
=>DC=4.10/7=40/7
Đúng 0
Bình luận (0)
b) \(\dfrac{S_{ADB}}{S_{ADC}}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)
Đúng 0
Bình luận (0)