Cho tầm giác ABC vuông tại A,AB<AC.Phân giác góc B cắt AC tại E.Trên BC lấy điểm I sao cho BA=BI.BE cắt AI tại H
a)Chứng minh:tam giác BAE=tam giác BIE
b)chứng minh:EI vuông góc với BC
c)chứng minh:BE vuông góc với AI
(Giải tầm giác vuông biết độ dài một cạnh và một góc nhọn)cho tam giác ABC vuông tại C có BC bằng 4cm và A bằng 30 độ a.hãy giải tam giác ABC B.tính tỉ số lượng giác của GÓC A
a: \(\widehat{B}=60^0\)
AB=8cm
\(AC=4\sqrt{3}\left(cm\right)\)
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Trực tâm của Tầm giác ABC vuông tại A là
Trực tâm của tam giác ABC vuông tại A là điểm A
bài 3;cho tam giác abc vuông tại a biết ab=2cm tính bc
bài 4;cho tam giác abc vuông tại a biết bc=2cm.tính ab,ac
bài 5.cho tam giác abc vuông tại a
a)tính ab biết bc=10cm,ac=8cm.b)tính ac biết bc=12 cm,ab=10cm
bài 1;cho tam giác abc vuông tại b. tính độ dài ab biết ac=12cm,bc=8cm
bài 2; cho tam giác mnp vuông tại n tính độ dài mn biết mb=căn bậc 30,np=căn bâc 14
bài 3;cho tam giác abc vuông tại a biết ab=2cm tính bc
baif4;cho tam giác abc vuông tại a biết bc=2cm.tính ab,ac
baif5.cho tam giác abc vuông tại a
a)tính ab biết bc=10cm,ac=8cm.b)tính ac biết bc=12 cm,ab=10cm
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BC^2+AB^2\)
\(\Leftrightarrow AB^2=AC^2-BC^2=12^2-8^2=80\)
hay \(AB=4\sqrt{5}cm\)
Vậy: \(AB=4\sqrt{5}cm\)
Bài 2:
Áp dụng định lí Pytago vào ΔMNP vuông tại N, ta được:
\(MP^2=MN^2+NP^2\)
\(\Leftrightarrow MN^2=MP^2-NP^2=\left(\sqrt{30}\right)^2-\left(\sqrt{14}\right)^2=16\)
hay MN=4cm
Vậy: MN=4cm
Bài 1 :
- Áp dụng định lý pi ta go ta được :\(BA^2+BC^2=AC^2\)
\(\Leftrightarrow AB^2+8^2=12^2\)
\(\Leftrightarrow AB=4\sqrt{5}\) ( cm )
Vậy ...
Bài 2 :
- Áp dụng định lý pi ta go vào tam giác MNP vuông tại N có :
\(MN^2+NP^2=MP^2\)
\(\Leftrightarrow MN^2+\sqrt{14}^2=\sqrt{30}^2\)
\(\Leftrightarrow MN=4\) ( đvđd )
Vậy ...
Cho tam giác ABC có BC= 1cm; AC= 7cm và độ dài cạnh AB là một số nguyên (cm).Tính độ dài AB và cho biết tam giác ABC là tam giác gì?
A. AB= 7cm và tam giác ABC vuông tại A
B. AB= 7cm và tam giác ABC cân tại A
C. AB= 7cm và tam giác ABC vuông cân tại A
D. AB= 8cm và tam giác ABC vuông tại B
Giải các tam giác vuông sau, tầm giác ABC vuông tại A biết: a)a=20;b=16 b)b=10;C=50° c)cos B=3/4;c=5
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB=\sqrt{20^2-16^2}=12\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=40^0\)
Xét ΔABC vuông tại A có
\(tanC=\dfrac{AB}{AC}\)
=>\(AB=10\cdot tan50\simeq11,92\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{10^2+11.92^2}\simeq15,56\left(cm\right)\)
c: Xét ΔABC vuông tại A có \(cosB=\dfrac{3}{4}\)
=>\(\dfrac{AB}{BC}=\dfrac{3}{4}\)
=>\(\dfrac{5}{BC}=\dfrac{3}{4}\)
=>\(BC=\dfrac{20}{3}\)
Xét ΔABC vuông tại A có cosB=3/4
nên \(\widehat{B}\simeq41^0\)
=>\(\widehat{C}=49^0\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(\dfrac{20}{3}\right)^2-5^2}=\dfrac{5\sqrt{7}}{3}\left(cm\right)\)
a, Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow AB=\sqrt{20^2-16^2}=12\)
\(cosB=\dfrac{AB}{BC}=\dfrac{12}{20}\Rightarrow\widehat{B}=53^o8'\)
\(cosC=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{C}=36^o52'\)
b, Vì tam giác ABC vuông tại A
\(\widehat{B}+\widehat{C}=90^o\\ \Rightarrow\widehat{B}=90^o-50^o=40^o\)
\(cosC=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{cosC}=\dfrac{10}{cos50^o}\approx15,6\)
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=tanC\times AC=tan50^o\times10\approx11,9\)
c,
\(cosB=\dfrac{AB}{BC}\\ \Rightarrow BC=\dfrac{AB}{cosB}=\dfrac{5}{\dfrac{3}{4}}=\dfrac{20}{3}\)
Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow AC=\sqrt{\left(\dfrac{20}{3}\right)^2-5^2}=\dfrac{5\sqrt{7}}{3}\)
\(cosB=\dfrac{3}{4}\Rightarrow\widehat{B}=41^o25'\\ sinC=\dfrac{AB}{BC}=\dfrac{5}{\dfrac{20}{3}}=48^o35'\)
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
a) Xét \(\Delta ABC\) vuông tại `A`
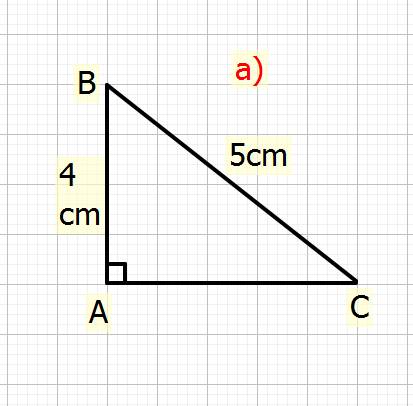
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
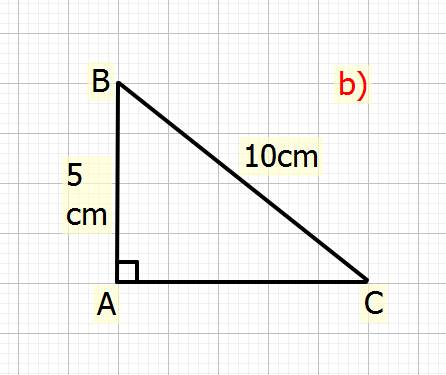
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
bài 1 :Cho tam giác ABC vuông tại A có AB =AC. Gọi d là đường thẳng bất kì đi qua A và cắt BC tại M. Kẻ BH vuông d tại H , CK vuông d tại K . chứng minh tam giác BHA = tam giác AKC
bài 2 :Cho tam giác ABC vuông tại A ( AB <AC). . Kẻ AH vuông BC tại H , trên AB lấy l sao cho lA=AC.Kẻ lK vuông góc với KH tại K.chứng minh tam giác AHC=lKA
1:
góc BAH+góc KAC=90 độ
góc BAH+góc ABH=90 độ
=>góc KAC=góc ABH
Xét ΔHBA vuông tại H và ΔKAC vuông tại K có
BA=AC
góc ABH=góc CAK
=>ΔHBA=ΔKAC