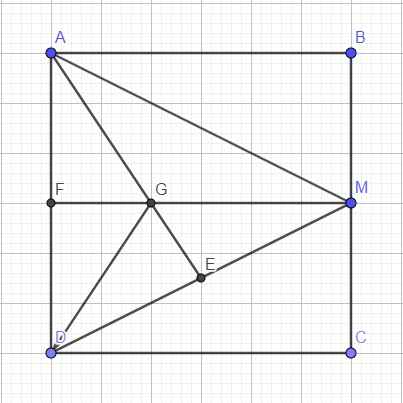
Cho hình vuông ABCD cạnh a Gọi M là trung điểm của BC Tính độ dài vectơ AM + BC

Những câu hỏi liên quan
Cho hình vuông ABCDcó cạnh a . Gọi I là trung điểm của cạnh BC . Tính độ dài của vectơ u=2AI-3AD theo a
I là trung điểm BC \(\Rightarrow\overrightarrow{BI}=\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AD}\Rightarrow2\overrightarrow{BI}=\overrightarrow{AD}\)
\(\overrightarrow{u}=2\left(\overrightarrow{AB}+\overrightarrow{BI}\right)-3\overrightarrow{AD}=2\overrightarrow{AB}+2\overrightarrow{BI}-3\overrightarrow{AD}=2\overrightarrow{AB}-2\overrightarrow{AD}=2\left(\overrightarrow{AB}+\overrightarrow{DA}\right)=2\overrightarrow{DB}\)
\(\Rightarrow\left|\overrightarrow{u}\right|=2\left|\overrightarrow{DB}\right|=2DB=2a\sqrt{2}\)
Đúng 2
Bình luận (2)
1 Hình vuông ABCD có cạnh AB=a. Gọi M là trung điểm của cạnh BC. Trên cạnh CD ta lấy điểm N sao cho khoảng cách từ đó đến đường thẳng AM bằng độ dài đoạn thẳng DN. Tính độ dài các đoạn thẳng AM, CN, MN
2 Cho tam giác vuông ABC vuông tại B có AB=3a, BC=4a. Ta dựng tam giác ACD vuông cân tại D sao cho D khác phía với B đối vớ đường thẳng AC. Tính độ dài AD,BD
Cho hình vuông ABCD có độ dài cạnh là 10 cm . Gọi O là tâm đường tròn nội tiếp hình vuông. Gọi M, N lần lượt là trung điểm của AB; BC. Tính độ dài của cung
M
N
⏜
? A. 2
π
(cm) B. 5
π
(cm) C. 2,5
π
(cm) D. 7,5
π
(cm)
Đọc tiếp
Cho hình vuông ABCD có độ dài cạnh là 10 cm . Gọi O là tâm đường tròn nội tiếp hình vuông. Gọi M, N lần lượt là trung điểm của AB; BC. Tính độ dài của cung M N ⏜ ?
A. 2 π (cm)
B. 5 π (cm)
C. 2,5 π (cm)
D. 7,5 π (cm)
Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
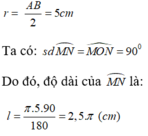
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a.Gọi M là trung điểm của BC.Tính độ dài vecto AM + vecto BC
\(\overrightarrow{AM}\cdot\overrightarrow{BC}=\overrightarrow{BC}\left(\overrightarrow{BM}-\overrightarrow{BA}\right)=\overrightarrow{BM}\cdot\overrightarrow{BC}-\overrightarrow{BC}\cdot\overrightarrow{BA}\)
\(=BM\cdot BC\cdot cos0^0=\dfrac{1}{2}\cdot a^2\cdot1=\dfrac{1}{2}a^2\)
\(\left|\overrightarrow{AM}+\overrightarrow{BC}\right|=\sqrt{AM^2+BC^2+2\cdot\dfrac{1}{2}a^2}\)
\(=\sqrt{\dfrac{1}{4}a^2+a^2+a^2+a^2}=\dfrac{\sqrt{13}}{2}\cdot a\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có độ dài cạnh bằng 6. Gọi M là trung điểm của BC và G là trọng tâm tam giác ADM. Tính độ dài vecto GD
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB=AC=7,5cm và BC=9cm. Gọi M là trung điểm của cạnh BC
a) CMR : AM vuông góc với BC
b) Tính độ dài đoạn thẳng AM
c) Gọi N là trung điểm của cạnh AB. Tính độ dài đoạn thẳng MN
d) CMR : MN song song với AC
tự vẽ hình nhé
a) ta có: tam giác ABC cân tại A
,mà MB=MC
=> AM LÀ đg phân giác
=> am VUÔNG GÓC VỚI BC
b) AM là đg phân giác (cmt)
=> AM =1/2 BC= 9:2=4.5(cm)
c) ta có tam giác AMB là tam giac vuông (AM vuông góc với BC )
mà N là trg điểm của AB
=>MN là đg phân giác
=> MN=1/2AB=7.5:2=3.75(cm)
d)ta có: AB=AC=7.5(cm)
=>AB vuông với AC
mà MN vuông với AB
=>MN//AC
TK DÙM MINK NHOA
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh là 10, M là trung điểm của BC.
a) Tính giá trị của | vectơ AB+ vectơ AD| và vectơ DM. vectơ DA
b)Tìm tập hợp điểm P thỏa mãn vectơ PA.vectơ BC=10
2/Cho h ình thoi có độ dài hai đường chéo bằng 6cm và 8cm .Tính độ dài cạnh hình thoi?3/Cho hình thang ABCD có AB // CD, AB 4, CD 12.Tính độ dài đường TB của hình thang4/Tam giác ABC vuông tại A, BC 7cm, MB MC, M BC.Tính độ dài AM?5/Cho tam giác ABC có M,N theo thứ tự là trung điểm của AB và AC.Biết MN 4,5 cm.Tính độ dài cạnh BC.6/Cho hình thang ABCD (AB//CD),gọi E,F theo thứ tự là trung điểm của AD và BC.Biết EF 6cm, AB 4cm ,tính độ dài cạnh CD?7/Hình thang có độ dài đáy lớn gấp đôi đáy...
Đọc tiếp
2/Cho h ình thoi có độ dài hai đường chéo bằng 6cm và 8cm .Tính độ dài cạnh hình thoi?
3/Cho hình thang ABCD có AB // CD, AB = 4, CD = 12.Tính độ dài đường TB của hình thang
4/Tam giác ABC vuông tại A, BC = 7cm, MB = MC, M BC.Tính độ dài AM?
5/Cho tam giác ABC có M,N theo thứ tự là trung điểm của AB và AC.Biết MN = 4,5 cm.Tính độ dài cạnh BC.
6/Cho hình thang ABCD (AB//CD),gọi E,F theo thứ tự là trung điểm của AD và BC.Biết EF = 6cm, AB = 4cm ,tính độ dài cạnh CD?
7/Hình thang có độ dài đáy lớn gấp đôi đáy nhỏ . Độ dài đường trung bình là 12 cm. Tính độ dài 2 đáy.
8/Cho hình chữ nhật ABCD, hai đường chéo AC và BD cắt nhau tại O, biết AO = 3cm, Tính độ dài BD?
9/Cho ABC và một điểm O tuỳ ý . Vẽ A/B/C/ đối xứng với ABC qua điểm O .
10/Cho hình vuông ABCD có độ dài đường chéo bằng 10cm.Tính cạnh hình vuông?
11/Cho hình vuông ABCD có độ dài cạnh bằng 3.Tính độ dài đường chéo của hình vuông?
12/T ính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các
cạnh góc vuông bằng 3 cm v à 4 cm.
có làm thì mới có ăn
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.Câu 2: Cho hình thang cân ABCD, đáy lớn CD10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.Câu 4: Cho tam giác ABC vuông tại A, ABAC; gọi I là giao điểm các đường phân giác, M là...
Đọc tiếp
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
Câu 2: Cho hình thang cân ABCD, đáy lớn CD=10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.
Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.
Câu 4: Cho tam giác ABC vuông tại A, AB<AC; gọi I là giao điểm các đường phân giác, M là trung điểm BC . Cho biết góc BIM bằng 90°. Tính BC:AC:AB.
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
Đúng 1
Bình luận (0)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Đúng 0
Bình luận (0)