Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
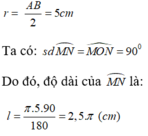
Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
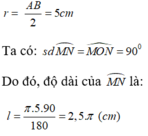
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
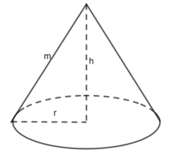
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
8.Cho đường tròn tâm O, đường kính AB = 13 cm. Dây CD có độ dài bằng 12 cm vuông góc
với AB tại H.
a) Tính độ dài HB, HA.
b) Gọi M và N lần lượt là hình chiếu của H trên AC, BC. Tính diện tích tứ giác CMHN.
cho hình vuông ABCD cạnh 5. Gọi M,N lần lượt là trung điểm của AB,BC. Gọi E là giao điểm của CM và DN. Chứng minh EM vuông góc với ED, từ đó chỉ ra tâm đường tròn qua 4 điểm A,D,E,N và bán kính đường tròn đó
Cho đường tròn (O) đường kính AB = 13 cm, dây CD có độ dài 12 cm vuông góc với AB tại H
a, Tính độ dài các đoạn thẳng HA, HB
b, Gọi M, N lần lượt là hình chiếu của H trên AC, BC. Tính diện tích tứ giác CMHN
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
Câu 2: Cho hình thang cân ABCD, đáy lớn CD=10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.
Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.
Câu 4: Cho tam giác ABC vuông tại A, AB<AC; gọi I là giao điểm các đường phân giác, M là trung điểm BC . Cho biết góc BIM bằng 90°. Tính BC:AC:AB.
Bài 1: Cho tam giác ABC nhọn ( AB<AC) nội tiếp đường tròn (O). Gọi H là hình chiếu vuông góc của A trên BC. Gọi M và N lần lượt là hình chiếu vuông góc của B và C trên đường kính AD của đường tròn(O)
a) CM tứ giác ABHM,AHNC nội tiếp
b) CM tam giác HMN đồng dạng tam giác ABC
c) Chứng minh HM vuông góc với AC
d) Gọi I là tủng điểm của BC. CM I là tâm đường tròn ngoại tiếp tam giác HMN
Bài 2:Cho đường tròn (O) đường kính AB=2R, Cl à trung điểm của OA và dây MN vuông góc với OA tại C. K là điểm di động trên cung nhỏ MB và H là giao của AK và MN
a) CM tứ giác BCHK nội tiếp
b) Chứng minh tam giác MBN đều
c) Tìm vị trí điểm K trên cung nhỏ MB sao cho KM+KN+KB đạt giá trị lớn nhất và tính giá trị lớn nhất đó theo R
Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( CM theo 2 tam giác nội tiếp)
Cho nửa đường tròn tâm O đường kình AB = 13 cm. dây cung CD có độ dài là 12 cm vuông với AB tại H
a) Tính HA ? HB ?
b) Gọi M,N theo thứ tự là hình chiếu của H trên AC, BC. Tính Diện tích của CMHN
Cho hình vuông ABCD độ dài cạnh là a. Gọi M, N lần lượt là trung điểm của AB, BC. Các đường thẳng DN và CM cắt nhau tại I. Chứng minh tam giác AID cân.