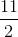Gọi H là trung điểm của DM
M là trung điểm của BC
=>\(BM=CM=\frac{BC}{2}=\frac{a}{2}\)
ΔMCD vuông tại C
=>\(CM^2+CD^2=DM^2\)
=>\(DM^2=a^2+\left(\frac{a}{2}\right)^2=\frac{5a^2}{4}\)
=>\(DM=\frac{a\sqrt5}{2}\)
ΔABM vuông tại B
=>\(AB^2+BM^2=AM^2\)
=>\(AM^2=a^2+\left(\frac{a}{2}\right)^2=\frac{5a^2}{4}\)
=>\(AM=\frac{a\sqrt5}{2}\)
Xét ΔAMD có AH là đường trung tuyến
nên \(AH^2=\frac{AD^2+AM^2}{2}-\frac{DM^2}{4}=\frac{a^2+\left(\frac{a\sqrt5}{2}\right)^2}{2}-\frac{\left(\frac{a\sqrt5}{2}\right)^2}{4}\)
\(=\frac12\left(a^2+\frac{_{}5a^2}{4}\right)-\frac14\cdot\frac{5a^2}{4}=\frac12a^2+\frac58a^2-\frac{5}{16}a^2=\frac{13}{16}a^2\)
=>\(AH=\frac{a\sqrt{13}}{4}\)
\(\left|\overrightarrow{AM}+\overrightarrow{BC}\right|=\left|\overrightarrow{AM}+\overrightarrow{AD}\right|=2\cdot\left|\overrightarrow{AH}\right|=2\cdot AH\)
\(=2\cdot\frac{a\sqrt{13}}{4}=\frac{a\sqrt{13}}{2}\)