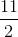E là trung điểmcủa BC
=>EB=EC=a/2
\(AE=\sqrt{AB^2+BE^2}=\dfrac{a\sqrt{5}}{2}\)
Xét ΔABE vuông tại B có \(\left\{{}\begin{matrix}cosBAE=\dfrac{AB}{AE}=\dfrac{a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{2}{\sqrt{5}}\\sinBAE=\dfrac{BE}{AE}=\dfrac{0.5a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
=>\(cosDAF=cosBEA=sinBAE=\dfrac{1}{\sqrt{5}}\)
\(AF=\dfrac{AE}{2}=\dfrac{a\sqrt{5}}{4}\)
Xét ΔADF có \(cosDAF=\dfrac{AD^2+AF^2-DF^2}{2\cdot AD\cdot AF}\)
=>\(\dfrac{a^2+a^2\cdot\dfrac{5}{16}-DF^2}{2\cdot\dfrac{a\sqrt{5}}{4}\cdot a}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{\dfrac{21}{16}a^2-DF^2}{\dfrac{a^2\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{21}{16}a^2-DF^2=\dfrac{a^2}{2}\)
=>\(DF^2=\dfrac{13}{16}a^2\)
=>\(DF=\dfrac{a\sqrt{13}}{4}\)