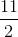Phương trình đường thẳng AM: \(ax+by-\dfrac{11}{2}a-\dfrac{1}{2}b=0\left(a^2+b^2\ne0\right)\)
Giả sử cạnh hình vuông có độ dài là \(a\)
\(AM^2=\dfrac{5}{4}a^2;AN^2=\dfrac{10}{9}a^2;MN^2=\dfrac{25}{36}a^2\)
Theo định lí cos: \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2.AM.AN}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{\left|2a-b\right|}{\sqrt{5\left(a^2+b^2\right)}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left(a-3b\right)\left(3a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\3a=-b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AM:3x+y-17=0\\AM:x-3y-4=0\end{matrix}\right.\)
TH1: \(AM:3x+y-17=0\Rightarrow A:\left\{{}\begin{matrix}3x+y-17=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(4;5\right)\)
TH2: \(AM:x-3y-4=0\Rightarrow A:\left\{{}\begin{matrix}x-3y-4=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(1;-1\right)\)