tìm số nguyên x biết: \(\dfrac{\sqrt{49}}{6}< \left|x-\dfrac{2}{3}\right|< -\dfrac{26}{\sqrt{81}}\)

Những câu hỏi liên quan
Cho a, b, x là những số dương. Đơn giản các biểu thức sau :
a) Aleft[dfrac{2a+left(abright)^{dfrac{1}{2}}}{3a}right]^{-1}left[dfrac{a^{dfrac{3}{2}}-b^{dfrac{3}{2}}}{a-left(abright)^{dfrac{1}{2}}}-dfrac{a-b}{sqrt{a}+sqrt{b}}right]
b) Bleft(dfrac{sqrt{a}-sqrt{x}}{sqrt{a+x}}-dfrac{sqrt{a+x}}{sqrt{a}+sqrt{x}}right)^{-2}-left(dfrac{sqrt{a}-sqrt{x}}{sqrt{a+x}}-dfrac{sqrt{a+x}}{sqrt{a}-sqrt{x}}right)^{-2}
c) Csqrt{16^{dfrac{1}{log_74}}+81^{dfrac{1}{log_69}}+15}
d) D49^{1-log_72}+5^{-log_54}
Đọc tiếp
Cho a, b, x là những số dương. Đơn giản các biểu thức sau :
a) \(A=\left[\dfrac{2a+\left(ab\right)^{\dfrac{1}{2}}}{3a}\right]^{-1}\left[\dfrac{a^{\dfrac{3}{2}}-b^{\dfrac{3}{2}}}{a-\left(ab\right)^{\dfrac{1}{2}}}-\dfrac{a-b}{\sqrt{a}+\sqrt{b}}\right]\)
b) \(B=\left(\dfrac{\sqrt{a}-\sqrt{x}}{\sqrt{a+x}}-\dfrac{\sqrt{a+x}}{\sqrt{a}+\sqrt{x}}\right)^{-2}-\left(\dfrac{\sqrt{a}-\sqrt{x}}{\sqrt{a+x}}-\dfrac{\sqrt{a+x}}{\sqrt{a}-\sqrt{x}}\right)^{-2}\)
c) \(C=\sqrt{16^{\dfrac{1}{\log_74}}+81^{\dfrac{1}{\log_69}}+15}\)
d) \(D=49^{1-\log_72}+5^{-\log_54}\)
1/ Giải phương trình sau:tan^2left(x+dfrac{pi}{3}right)+left(sqrt{3}-1right)tanleft(x+dfrac{pi}{3}right)-sqrt{3}02/ Tìm hệ số của số hạng chứa x^{26} trong khai triển left(dfrac{1}{x^4}+x^7right)^n . Biết C^2_{n+2}-4C^n_{n+1}2left(n+1right) (n ∈ N* ; x 0)
Đọc tiếp
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)
Câu 2:
\(\Leftrightarrow\dfrac{\left(n+2\right)!}{2!\cdot n!}-4\cdot\dfrac{\left(n+1\right)!}{n!\cdot1!}=2\left(n+1\right)\)
\(\Leftrightarrow\dfrac{\left(n+1\right)\left(n+2\right)}{2}-4\cdot\dfrac{n+1}{1}=2\left(n+1\right)\)
\(\Leftrightarrow\left(n+1\right)\left(n+2\right)-8\left(n+1\right)=4\left(n+1\right)\)
=>(n+1)(n+2-8-4)=0
=>n=-1(loại) hoặc n=10
=>\(A=\left(\dfrac{1}{x^4}+x^7\right)^{10}\)
SHTQ là: \(C^k_{10}\cdot\left(\dfrac{1}{x^4}\right)^{10-k}\cdot x^{7k}=C^k_{10}\cdot1\cdot x^{11k-40}\)
Số hạng chứa x^26 tương ứng với 11k-40=26
=>k=6
=>Số hạng cần tìm là: \(210x^{26}\)
Đúng 2
Bình luận (0)
Tìm số nguyên x biết
\(\frac{\sqrt{49}}{6}< \left|x-\frac{2}{3}\right|< \frac{26}{\sqrt{81}}\)
\(\Rightarrow\frac{7}{6}< |x-\frac{2}{3}|< \frac{26}{9}\)
\(\Rightarrow\frac{21}{18}< |x-\frac{2}{3}|< \frac{52}{18}\)
Rùi tự thay vào
Đúng 0
Bình luận (0)
\(\frac{\sqrt{49}}{6}< \left|x-\frac{2}{3}\right|< \frac{26}{\sqrt{81}}\)
\(\Leftrightarrow\frac{7}{6}< \left|x-\frac{2}{3}\right|< \frac{26}{9}\)
\(\Leftrightarrow\frac{7}{6}< 2\le\left|x-\frac{2}{3}\right|\le2< \frac{26}{9}\)
\(\Leftrightarrow\left|x-\frac{2}{3}\right|=2\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{2}{3}=2\\x-\frac{2}{3}=-2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{8}{3}\\x=--\frac{4}{3}\end{cases}}\)
Vậy \(x\in\left\{\frac{8}{3};-\frac{4}{3}\right\}\)
Cho biểu thức:
\(A=\left(1-\dfrac{\sqrt{x}}{\sqrt{x+1}}\right):\left(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{\sqrt{x}+2}{x-5\sqrt{x+6}}\right)\)
a) Rút gọn A
b) Tìm x để A<0
c) Tìm giá trị nhỏ nhất của A
d) Tính giá trị nguyên của x để A nhận giá trị nguyên
Tìm x để các căn bậc hai sau có nghĩa a) sqrt{dfrac{15+3x^2}{-6}} b) sqrt{dfrac{-81}{-12-x^2}} c) sqrt{dfrac{31left(x^2+21right)}{3}} d) sqrt{dfrac{-12}{11+x^2}} e) sqrt{dfrac{21}{-x^2-17}}
Đọc tiếp
Tìm x để các căn bậc hai sau có nghĩa
a) \(\sqrt{\dfrac{15+3x^2}{-6}}\) b) \(\sqrt{\dfrac{-81}{-12-x^2}}\)
c) \(\sqrt{\dfrac{31\left(x^2+21\right)}{3}}\) d) \(\sqrt{\dfrac{-12}{11+x^2}}\)
e) \(\sqrt{\dfrac{21}{-x^2-17}}\)
a: ĐKXĐ: 3x^2+15/-6>=0
=>3x^2+15<=0(vô lý)
b: ĐKXĐ: -81/-x^2-12>=0
=>-x^2-12<0
=>-x^2<12
=>x^2>-12(luôn đúng)
c: ĐKXĐ: 31(x^2+21)/3>=0
=>x^2+21>=0(luôn đúng)
d: ĐKXĐ: -12/x^2+11>=0
=>x^2+11<0(vô lý)
e: ĐKXĐ: 21/-x^2-17>=0
=>-x^2-17>0
=>x^2+17<0(vô lý)
Đúng 0
Bình luận (0)
Cho biểu thức \(M=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{6\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\) với \(x\ge0;x\ne1\)
a. Rút gọn M
b. Tìm số nguyên x để M có giá trị là số nguyên
a) \(M=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{6\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\left(x\ge0,x\ne1\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-6\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{x-4\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)
b) \(M=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}=1-\dfrac{5}{\sqrt{x}+2}\in Z\)
\(\Rightarrow\sqrt{x}+2\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(\sqrt{x}\ge0\forall x\)
\(\Rightarrow\sqrt{x}\in\left\{3\right\}\Rightarrow x=9\left(tm\right)\)
Đúng 0
Bình luận (0)
\(\left(\dfrac{2\sqrt{x}}{\sqrt{x+3}}+\dfrac{\sqrt{x}}{\sqrt{x-3}}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{\sqrt{x-1}}{\sqrt{x-3}}-\dfrac{1}{2}\right)\)
rút gọn A
tìm các giá trị x nguyên để biểu thức trên nguyên
6.A=\(\left(\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}\right):\dfrac{2\left(x-2\sqrt{x}+1\right)}{\sqrt{x}-1}\)
a) Rút gọn A
b)Tìm a ϵ Z để biểu thức A nhận giá trị nguyên
a) Ta có: \(A=\left(\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}\right):\dfrac{2\left(x-2\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{2\left(\sqrt{x}-1\right)+2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}:\dfrac{2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)}\)
\(=\dfrac{4\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{1}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)^2}\)
Đúng 2
Bình luận (0)
\(\left(\dfrac{1}{\sqrt{x}}-\sqrt{x}\right):\left(\dfrac{1-\sqrt[]{x}}{x+\sqrt{x}}\right)\)
\(\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}-3}\)
\(\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
RÚT GON
\(\left(\dfrac{1}{\sqrt{x}}-\sqrt{x}\right):\left(\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\) (ĐK: \(x>0\))
\(=\left(\dfrac{1}{\sqrt{x}}-\dfrac{x}{\sqrt{x}}\right)\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{-\sqrt{x}}\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{-\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\left(\sqrt{x}+1\right)^2\)
Đúng 1
Bình luận (0)
c: 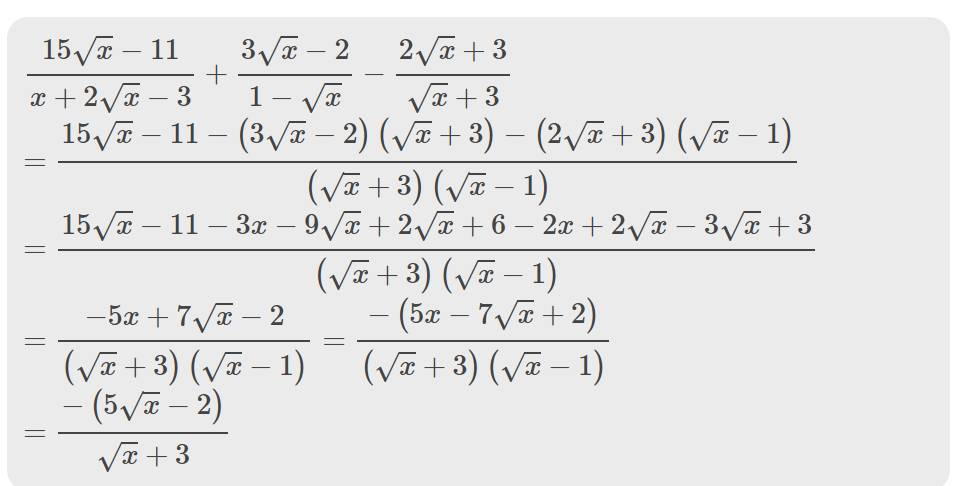
b;
Sửa đề: \(\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2\sqrt{x}\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2x-6\sqrt{x}+x-4\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}-x+16\sqrt{x}-16}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{x+16}{\sqrt{x}+3}\)
Đúng 1
Bình luận (0)

















